题目内容
4.如图1,对于平面内小于等于90°的∠MON,我们给出如下定义:若点P在∠MON的内部或边上,作PE⊥OM于点E,PF⊥ON于点F,则将PE+PF称为点P与∠MON的“点角距”,记作d(∠MON,P).如图2,在平面直角坐标系xOy中,x、y正半轴所组成的角为∠xOy.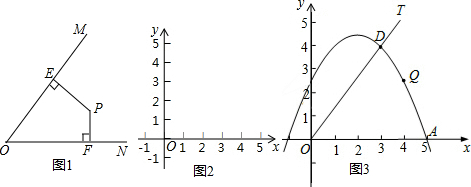
(1)已知点A(5,0)、点B(3,2),则d(∠xOy,A)=5,d(∠xOy,B)=5.
(2)若点P为∠xOy内部或边上的动点,且满足d(∠xOy,P)=5,在图2中画出点P运动所形成的图形.
(3)如图3,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}{x}^{2}$+mx+n经过A(5,0)与点D(3,4)两点,点Q是A、D两点之间的抛物线上的动点(点Q可与A、D两点重合),求当d(∠xOD,Q)取最大值时点Q的坐标.
分析 (1)根据若点P在∠MON的内部或边上,作PE⊥OM于点E,PF⊥ON于点F,则将PE+PF称为点P与∠MON的“点角距”,记作d(∠MON,P),可得答案;
(2)根据点P为∠xOy内部或边上的动点,且满足d(∠xOy,P)=5,可得函数,根据函数,可得函数图象;
(3)根据相似三角形的判定与性质,可得QE的长,根据d(∠xOD,Q),可得二次函数,根据二次函数的性质,可得答案.
解答 28.(1)已知点A(5,0)、点B(3,2),则d(∠xOy,A)=5,d(∠xOy,B)=5.
故答案为:5,5;
(2)过B点的直线为y=-x+5,如图1, ;
;
(3)过点Q作QF⊥x轴于F,QE⊥OD于E,延长FQ交OD于M,如图2, ,
,
可求直线OD表达式为:y=$\frac{4}{3}$x,
抛物线表达式为:y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$,
设Q(x,-$\frac{1}{2}$x2+2x+$\frac{5}{2}$),则M(x,$\frac{4}{3}$x)
∴MQ=$\frac{1}{2}$x2-$\frac{2}{3}$x-$\frac{5}{2}$.
在Rt△MOF中,利用勾股定理可求OM=$\sqrt{O{F}^{2}+F{M}^{2}}$=$\frac{5x}{3}$.
利用△MEQ∽△MFO,可得:$\frac{MQ}{MO}$=$\frac{QE}{OF}$
即:$\frac{\frac{1}{2}{x}^{2}-\frac{2}{3}x-\frac{5}{2}}{\frac{5x}{3}}$=$\frac{QE}{x}$
∴QE=$\frac{3}{10}$x2-$\frac{2}{5}$x-$\frac{3}{2}$,
∴QE+QF=($\frac{3}{10}$x2-$\frac{2}{5}$x-$\frac{3}{2}$)+(-$\frac{1}{2}$x2+2x+$\frac{5}{2}$)
=-$\frac{1}{5}$x+$\frac{8}{5}$x+1
=-$\frac{1}{5}$(x-4)2+$\frac{21}{5}$ (3≤x≤5),
∴当x=4时,QE+QF的值最大,最大值为$\frac{21}{5}$,此时Q点坐标为(4,$\frac{5}{2}$).
点评 本题考查了二次函数综合题,利用若点P在∠MON的内部或边上,作PE⊥OM于点E,PF⊥ON于点F,则将PE+PF称为点P与∠MON的“点角距”,记作d(∠MON,P)是解题关键;利用相似三角形的判定与性质得出EQ的长是解题关键.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5,-1,-3,-1.则下列结论错误的是( )
| A. | 方差是8 | B. | 中位数是-1 | C. | 众数是-1 | D. | 平均数是0 |
| A. | m>-1.5 | B. | m<-1.5 | C. | m>1.5 | D. | m<1.5 |
| A. |  | B. |  | C. |  | D. |  |
| A. | 3a+2a=5a2 | B. | -x2•(-x)3=(-x)5 | C. | 2a2•a3=2a6 | D. | (a-b)(b-a)=-(a-b)2 |