题目内容

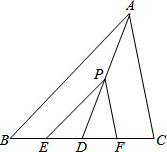设点P是△ABC中线AD上一点，过P作AB、AC的平行线EP、FP分别交BC于点E、F，求证：BE=CF．
考点：相似三角形的判定与性质
专题：证明题
分析：利用平行可得到
DE
BD
=
DP
DA
=
DF
DC
，结合条件可得DE=DF，可证得BE=CF．
解答：证明：
∵PE∥AB，PF∥AC
∴
DE
BD
=
DP
DA
=
DF
DC
，
∵AD为中线，
∴BD=DA，
∴DE=DF，
∴BE=CF．
点评：本题主要考查平行线分线段成比例，掌握平行线分线段所得线段对应成比例是解题的关键．
练习册系列答案
相关题目
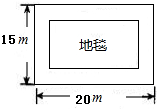一间会议室，它的地面是长方形的，长为20m，宽为15m，现在准备在会议室地面的中间铺一块地毯，要求四周未铺地毯的部分宽度相等，而且地毯的面积是会议室地面面积的一半，则地面上未铺地毯的部分宽度是多米？
如图，AB、BF分别是⊙O的直径和弦，弦CD与AB、BF分别相交于点E、G，过点F的切线HF与DC的延长线相交于点H，且AB⊥CD．
（1）求证：HF=HG；
（2）若sin∠HGF=
3
4
，BF=3，求⊙O的半径长．
一家电子计算器专卖店搞促销活动，将每只进价为40元，售价60元的计算机按以下方式进行优惠：凡是一次买10只以上的，每多买1只，所买的全部计算器每只就降低1元，例如，某人买20只计算器，于是每只降价1×（20-10）=10（元），因此，所买的全部20只计算器都按照每只50元计算，但是最低价为每只46元．
（1）若一次至少买m只，才能以最低价购买，求m的值；
（2）写出该专卖店当一次销售x只（x＞10）时，所获利润y（元）与x（只）之间的函数关系式；
（3）有一天，一位顾客买了18只，另一位顾客买了20只，结果店主发现卖了20只反而比卖了18只赚的钱少，为了使每次卖的多赚钱也多，在其他促销条件不变的情况下，最低价每只46元要提高到多少？为什么？
如图，已知AB切⊙O于点A，OB⊥AC于点C，交⊙O于点D，连接AD，求证：∠1=∠2．
如图所示，直线PD为△ABC一边BC的垂直平分线，点D为垂足，连接CP并延长CP交边AB于点F，射线BP交边AC于点E．
（1）若∠A=∠BPF，求证：BF=CE．
（2）在（1）的条件下，若∠A=60°，线段PD、PE、PF之间的数量关系为
 
．
（3）在（2）的条件下，若PC=8，且PF•PE=9，（PF＞PE），求PF-PE的值．
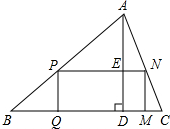如图，在△ABC中，AD是高，矩形PQMN的顶点P、N分别在AB、AC上，QM在BC上，AD交PN于点E．设BC=48，AD=16，PQ：PN=5：9，求矩形PQMN的面积．
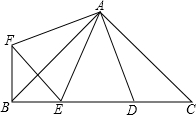如图，∠BAC=∠DAF=90°，AB=AC=3
2
，AD=AF，点D、E为BC边上的两点，且∠DAE=45°，连接EF、BF．
（1）求证：△AED≌△AEF；
（2）若BE=2，求DE的长．
如图所示，在平面直角坐标系中xOy中，抛物线y=mx2-2mx-2（m≠0）与y轴交于点A，其对称轴与x轴交于点B
（1）求点A，B的坐标；
（2）若直线l与直线AB关于该抛物线的对称轴对称，该抛物线在-2＜x＜-1这一段位于直线l的上方，并且在2＜x＜3这一段位于直线AB的下方，求该抛物线的解析式；
（3）（2）中抛物线上两点P、Q，若点P、Q绕某点逆时针旋转90°相应得P1（-6，-1）、Q1（0，0）两点，求以PQ为对角线的正方形的另两个顶点坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网