题目内容
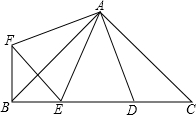 如图,∠BAC=∠DAF=90°,AB=AC=3
如图,∠BAC=∠DAF=90°,AB=AC=3| 2 |
(1)求证:△AED≌△AEF;
(2)若BE=2,求DE的长.
考点:全等三角形的判定与性质
专题:
分析:(1)易证∠FAE=45°,即可证明△AED≌△AEF,即可解题;
(2)易证∠BAF=∠CAD,即可证明△ABF≌△ACD,可得∠ABF=∠C=45°,CD=BF,再根据(1)中结论可得EF=DE,根据BF2+BE2=EF2和DE+CD=4,即可求得EF的长,即可解题.
(2)易证∠BAF=∠CAD,即可证明△ABF≌△ACD,可得∠ABF=∠C=45°,CD=BF,再根据(1)中结论可得EF=DE,根据BF2+BE2=EF2和DE+CD=4,即可求得EF的长,即可解题.
解答:(1)证明:∵∠DAF=90°,∠DAE=45°,
∴∠FAE=∠DAF-∠DAE=45°.
在△AED与△AEF中,
,
∴△AED≌△AEF(SAS);
(2)解:∵∠BAC=90°,AB=AC=3
,
∴BC=6,∠ABC=∠C=45°,
∵∠BAC=∠DAF=90°,∠BAD+∠BAF=∠DAF,∠BAD+∠CAD=∠BAC,
∴∠BAF=∠CAD,
在△ABF和△ACD中,
,
∴△ABF≌△ACD,(SAS)
∴∠ABF=∠C=45°,CD=BF,
∴∠EBF=90°,
∵△AED≌△AEF,
∴EF=DE,
∵BF2+BE2=EF2,DE+CD=EF+BF=BC-BE=4,
∴DE=EF=
,BF=
.
∴∠FAE=∠DAF-∠DAE=45°.
在△AED与△AEF中,
|
∴△AED≌△AEF(SAS);
(2)解:∵∠BAC=90°,AB=AC=3
| 2 |
∴BC=6,∠ABC=∠C=45°,
∵∠BAC=∠DAF=90°,∠BAD+∠BAF=∠DAF,∠BAD+∠CAD=∠BAC,
∴∠BAF=∠CAD,
在△ABF和△ACD中,
|
∴△ABF≌△ACD,(SAS)
∴∠ABF=∠C=45°,CD=BF,
∴∠EBF=90°,
∵△AED≌△AEF,
∴EF=DE,
∵BF2+BE2=EF2,DE+CD=EF+BF=BC-BE=4,
∴DE=EF=
| 5 |
| 2 |
| 3 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△AED≌△AEF和△ABF≌△ACD是解题的关键.

练习册系列答案
相关题目
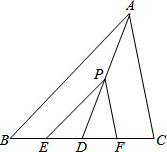 设点P是△ABC中线AD上一点,过P作AB、AC的平行线EP、FP分别交BC于点E、F,求证:BE=CF.
设点P是△ABC中线AD上一点,过P作AB、AC的平行线EP、FP分别交BC于点E、F,求证:BE=CF.
 如图所示,点C、D为线段AB的三等分点,点E为线段AC的中点,若EC=3,求线段AB的长度.
如图所示,点C、D为线段AB的三等分点,点E为线段AC的中点,若EC=3,求线段AB的长度.