题目内容
 如图,已知AB切⊙O于点A,OB⊥AC于点C,交⊙O于点D,连接AD,求证:∠1=∠2.
如图,已知AB切⊙O于点A,OB⊥AC于点C,交⊙O于点D,连接AD,求证:∠1=∠2.考点:切线的性质
专题:证明题
分析:连接AO,由切线的性质定理可得∠1+∠OAD=90°,由OB⊥AC,可得∠2+∠CDA=90°,又因为OD=OA,所以可得∠OAD=∠CDA,进而可证明∠1=∠2.
解答:证明:连接AO,
∵AB切⊙O于点A,
∴∠OAB=90°,
∴∠1+∠OAD=90°,
∵OB⊥AC,
∴∠2+∠CDA=90°,
又∵OD=OA,
∴∠OAD=∠CDA,
∴∠1=∠2.

∵AB切⊙O于点A,
∴∠OAB=90°,
∴∠1+∠OAD=90°,
∵OB⊥AC,
∴∠2+∠CDA=90°,
又∵OD=OA,
∴∠OAD=∠CDA,
∴∠1=∠2.
点评:本题考查了切线的性质定理、垂直的性质以及圆的有关性质,解题的关键是挖掘题目的隐藏条件:圆的半径处处相等.

练习册系列答案
相关题目
H7N9型禽流感是全球首次发现的新亚型流感病毒,与其他微生物相比,病毒的形态极其微小,一个一般大小的细菌,直径为500纳米,而大多数病毒的直径在10-300纳米,所以它可以通过细菌过滤器,将300纳米用科学记数法表示为( )
| A、0.3×10-10米 |
| B、3×10-11米 |
| C、3×10-7米 |
| D、30×10-7米 |
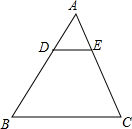 如图,△在ABC中,DE∥BC,若DE:BC=1:3,则△ADE与△ABC的周长之比是
如图,△在ABC中,DE∥BC,若DE:BC=1:3,则△ADE与△ABC的周长之比是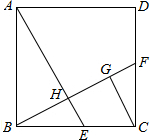 如图,在正方形ABCD中,E,F分别是边BC、CD的中点,AE交BF于点H,CG∥AE交BF于点G,给出下列结论:①△BHE为直角三角形;②CG•BF=BC•CF;③BH=FG;④
如图,在正方形ABCD中,E,F分别是边BC、CD的中点,AE交BF于点H,CG∥AE交BF于点G,给出下列结论:①△BHE为直角三角形;②CG•BF=BC•CF;③BH=FG;④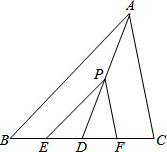 设点P是△ABC中线AD上一点,过P作AB、AC的平行线EP、FP分别交BC于点E、F,求证:BE=CF.
设点P是△ABC中线AD上一点,过P作AB、AC的平行线EP、FP分别交BC于点E、F,求证:BE=CF.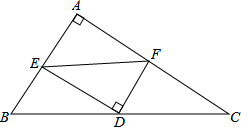 如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.
如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长. 如图所示,点C、D为线段AB的三等分点,点E为线段AC的中点,若EC=3,求线段AB的长度.
如图所示,点C、D为线段AB的三等分点,点E为线段AC的中点,若EC=3,求线段AB的长度.