题目内容
 如图,AB、BF分别是⊙O的直径和弦,弦CD与AB、BF分别相交于点E、G,过点F的切线HF与DC的延长线相交于点H,且AB⊥CD.
如图,AB、BF分别是⊙O的直径和弦,弦CD与AB、BF分别相交于点E、G,过点F的切线HF与DC的延长线相交于点H,且AB⊥CD.(1)求证:HF=HG;
(2)若sin∠HGF=
| 3 |
| 4 |
考点:切线的性质
专题:
分析:(1)连接AF,根据切线的性质求得∠BFH=∠FAB,根据直角三角形的性质首先求出∠BGE=∠FAB,进而得出∠BFH=∠FGH,根据等角对等边即可得出HF=HG;
(2)根据∠HGF=∠A,利用锐角三角函数得出AB即可得出半径.
(2)根据∠HGF=∠A,利用锐角三角函数得出AB即可得出半径.
解答: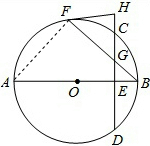 (1)证明:如图,连接AF,
(1)证明:如图,连接AF,
∵HF是⊙O的切线,
∴∠BFH=∠FAB,
∵AB是直径,
∴∠AFB=90°,
∴∠FAB+∠FBA=90°.
∵AB⊥CD.
∴∠BGE+∠FBA=90°,
∴∠BGE=∠FAB,
∵∠FGH=∠BGE,
∴∠BFH=∠FGH,
∴HF=HG;
(2)解:∵∠AFB=90°,∠HGF=∠FAB,
∴sin∠HGF=sin∠FAB=
=
,
∴AB=
=
=4.
∴⊙O的半径长为2.
 (1)证明:如图,连接AF,
(1)证明:如图,连接AF,∵HF是⊙O的切线,
∴∠BFH=∠FAB,
∵AB是直径,
∴∠AFB=90°,
∴∠FAB+∠FBA=90°.
∵AB⊥CD.
∴∠BGE+∠FBA=90°,
∴∠BGE=∠FAB,
∵∠FGH=∠BGE,
∴∠BFH=∠FGH,
∴HF=HG;
(2)解:∵∠AFB=90°,∠HGF=∠FAB,
∴sin∠HGF=sin∠FAB=
| BF |
| AB |
| 3 |
| 4 |
∴AB=
| 4BF |
| 3 |
| 4×3 |
| 3 |
∴⊙O的半径长为2.
点评:此题主要考查了圆的综合应用以及切线的判定与性质和锐角三角函数应用,根据已知得出∠HGF=∠BGE=∠A是解题关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 如图:每个小正方形的边长均为a,连接小正方形的三个顶点得△ABC,则AB边上的高是( )
如图:每个小正方形的边长均为a,连接小正方形的三个顶点得△ABC,则AB边上的高是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
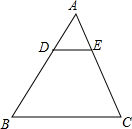 如图,△在ABC中,DE∥BC,若DE:BC=1:3,则△ADE与△ABC的周长之比是
如图,△在ABC中,DE∥BC,若DE:BC=1:3,则△ADE与△ABC的周长之比是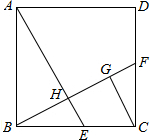 如图,在正方形ABCD中,E,F分别是边BC、CD的中点,AE交BF于点H,CG∥AE交BF于点G,给出下列结论:①△BHE为直角三角形;②CG•BF=BC•CF;③BH=FG;④
如图,在正方形ABCD中,E,F分别是边BC、CD的中点,AE交BF于点H,CG∥AE交BF于点G,给出下列结论:①△BHE为直角三角形;②CG•BF=BC•CF;③BH=FG;④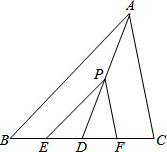 设点P是△ABC中线AD上一点,过P作AB、AC的平行线EP、FP分别交BC于点E、F,求证:BE=CF.
设点P是△ABC中线AD上一点,过P作AB、AC的平行线EP、FP分别交BC于点E、F,求证:BE=CF.