题目内容
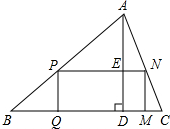如图，在△ABC中，AD是高，矩形PQMN的顶点P、N分别在AB、AC上，QM在BC上，AD交PN于点E．设BC=48，AD=16，PQ：PN=5：9，求矩形PQMN的面积．考点：相似三角形的判定与性质,矩形的性质
专题：
分析：设PQ=5x，则PN=9x，利用PN∥BC，可得到
=
，代入可求得x，再计算矩形PQMN的面积即可．
| PN |
| BC |
| AE |
| AD |
解答：解：
∵PQ：PN=5：9，
∴设PQ=5x，则PN=9x，
∵四边形PQMN为矩形，
∴ED=PQ=5x，AE=AD-DE=16-5x
又PN∥BC，
∴
=
，即
=
，
解得x=2，
∴PQ=10，PN=18，
∴S矩形PQMN=PQ•PN=10×18=180．
∵PQ：PN=5：9，
∴设PQ=5x，则PN=9x，
∵四边形PQMN为矩形，
∴ED=PQ=5x，AE=AD-DE=16-5x
又PN∥BC，
∴
| AE |
| AD |
| PN |
| BC |
| 16-5x |
| 16 |
| 9x |
| 48 |
解得x=2，
∴PQ=10，PN=18，
∴S矩形PQMN=PQ•PN=10×18=180．
点评：本题主要考查平行线分线段成比例和矩形的性质，掌握平行线分线段所得线段对应成比例是解题的关键．
练习册系列答案
同步奥数系列答案
相关题目
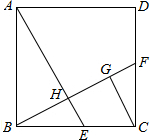如图，在正方形ABCD中，E，F分别是边BC、CD的中点，AE交BF于点H，CG∥AE交BF于点G，给出下列结论：①△BHE为直角三角形；②CG•BF=BC•CF；③BH=FG；④
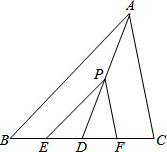设点P是△ABC中线AD上一点，过P作AB、AC的平行线EP、FP分别交BC于点E、F，求证：BE=CF．
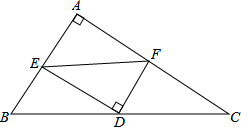如图，△ABC中，∠A=90°，D为斜边BC的中点，E、F分别为AB、AC上的点，且DE⊥DF．若BE=3，CF=4，试求EF的长．
如图所示，点C、D为线段AB的三等分点，点E为线段AC的中点，若EC=3，求线段AB的长度．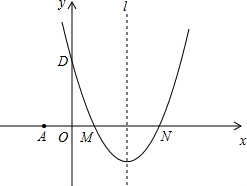
如图，在平面直角坐标系中，抛物线y=x2-4x+3的图象与x轴交于M和N两点，且与y轴交于D，直线l是抛物线的对称轴．