题目内容
1. 正方形网格中,∠AOB如图放置,则tan∠AOB的值为( )
正方形网格中,∠AOB如图放置,则tan∠AOB的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 根据图形连接AC,分别求出AC、OC、AO的长度,可得△OAC为直角三角形,继而求出tan∠AOB的值.
解答 解:如图,AC=$\sqrt{1+{3}^{2}}$=$\sqrt{10}$,OC=$\sqrt{1+{3}^{2}}$=$\sqrt{10}$,OC=$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{20}$,
∵AC2+OC2=20=OC2,
∴△OAC为直角三角形,
∵AC=OC,
∴△OAC为等腰直角三角形,
∴tan∠AOB=tan45°=1.
故选B.
点评 本题考查了特殊角的三角函数值,解答本题的关键是根据题意判断三角形OAC为等腰直角三角形.

练习册系列答案
相关题目
12. 如图,AB∥CD,CB平分∠ECD交AB于点B,若∠ECD=60°,则∠B的度数为( )
如图,AB∥CD,CB平分∠ECD交AB于点B,若∠ECD=60°,则∠B的度数为( )
 如图,AB∥CD,CB平分∠ECD交AB于点B,若∠ECD=60°,则∠B的度数为( )
如图,AB∥CD,CB平分∠ECD交AB于点B,若∠ECD=60°,则∠B的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
16.已知两点A(7,4),B(5,2),先将线段AB向左平移一个单位,再以原点O为位似中心,在第一象限内将其缩小为原来的$\frac{1}{2}$得到线段CD,则点A的对应点C的坐标为( )
| A. | (2,3) | B. | (3,2) | C. | (2,1) | D. | (3,3) |
6.下列方程中是一元二次方程的是( )
| A. | 2x+1=0 | B. | x2+2x=x2-1 | C. | ax2+bx+c=0 | D. | 3(x+1)2=2(x+1) |
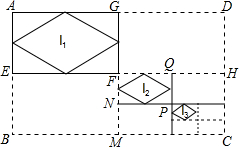 如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是$\frac{3}{8}$cm2.
如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是$\frac{3}{8}$cm2. 如图,四边形ABCD中,BD平分∠ABC,AD=DC,求证:∠A与∠C互补.
如图,四边形ABCD中,BD平分∠ABC,AD=DC,求证:∠A与∠C互补.