题目内容
9.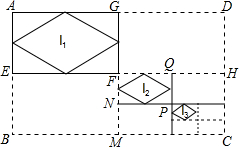 如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是$\frac{3}{8}$cm2.
如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是$\frac{3}{8}$cm2.
分析 根据题意和菱形的面积公式求出菱形l1的面积,根据中点的性质进行计算即可求出菱形l4的面积.
解答 解:∵矩形ABCD的长和宽分别为16cm和12cm,
∴EF=8cm,AE=6cm,
∴菱形l1的面积=$\frac{1}{2}$×8×6=24cm2,
同理,菱形l2的面积=$\frac{1}{2}$×4×3=6cm2,
则菱形l3的面积=$\frac{1}{2}$×2×$\frac{3}{2}$=$\frac{3}{2}$cm2,
∴菱形l4的面积=$\frac{1}{2}$×1×$\frac{3}{4}$=$\frac{3}{8}$cm2,
故答案为:$\frac{3}{8}$.
点评 本题考查的是中点四边形的性质,掌握菱形的面积公式、通过计算找出规律是解题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
17.若单项式-2amb7与5a2b2m+n是同类项,则(-m)n的值是( )
| A. | 2 | B. | 6 | C. | 8 | D. | -8 |
1. 正方形网格中,∠AOB如图放置,则tan∠AOB的值为( )
正方形网格中,∠AOB如图放置,则tan∠AOB的值为( )
 正方形网格中,∠AOB如图放置,则tan∠AOB的值为( )
正方形网格中,∠AOB如图放置,则tan∠AOB的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
18.为了调查某一路口某时段的汽车流量,记录了10天这一时段通过该路口的汽车辆数,其中有2天是142辆,2天是145辆,3天是150辆,1天是154辆,2天是156辆.那么这10天在该时段通过该路口汽车平均辆数为( )
| A. | 148 | B. | 149 | C. | 150 | D. | 151 |
19.下列说法正确的是( )
| A. | 近似数1.50和1.5是相同的 | B. | 300万精确到百分位 | ||
| C. | 6.610精确到千分位 | D. | 2.70×104精确到百分位 |




 小明一家三口国庆节随旅游团去九寨沟旅游,共花费人民币5600元,他把旅途费用支出情况制成了如下的统计图.请你根据统计图解决下列问题:
小明一家三口国庆节随旅游团去九寨沟旅游,共花费人民币5600元,他把旅途费用支出情况制成了如下的统计图.请你根据统计图解决下列问题: