题目内容
5.已知,点D位直线BC上一动点(点D不与点B,C重合),∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,∠DAE=90°,AD=AE,连接CE.(1)如图1,当点D在线段BC上时,求证:
①BD⊥CE;
②CE=BC-CD.
知识迁移,探究发现
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CE,BC,CD三条线段之间的数量关系.

分析 (1)如图1中,只要证明△ABD≌△ACE,即可得到∠ABD=∠ACE=45°,BD=CE,由此可以证明.
(2)如图2中,结论:CE=BC+CD,证明方法类似(1).
解答 (1)证明:如图1中,∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE=45°,BD=CE,
∴∠ACB+∠ACE=90°
∴∠ECB=90°,
∴BD⊥CE,CE=BC-CD.
(2)如图2中,结论:CE=BC+CD,理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CE=BC+CD.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是正确寻找全等三角形,属于中考常考题型.

练习册系列答案
相关题目
15.某班7名同学在一学期里阅读课外书籍的册数分别是:14,12,13,12,17,18,16.则这组数据的众数和中位数分别是( )
| A. | 12,14 | B. | 12,13 | C. | 13,14 | D. | 13,16 |

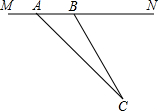 “为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m. 如图,?ABCD对角线AC、BD相交于点O,E、F分别是OA、OC的中点;
如图,?ABCD对角线AC、BD相交于点O,E、F分别是OA、OC的中点;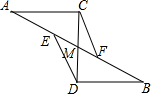 如图,AC=BD,∠A=∠B,点E、F在AB上,且DE∥CF,CD与AB交于点M,小明经过研究发现该图形是中心对称图形,则该图形的对称中心是点M.
如图,AC=BD,∠A=∠B,点E、F在AB上,且DE∥CF,CD与AB交于点M,小明经过研究发现该图形是中心对称图形,则该图形的对称中心是点M.