题目内容
14.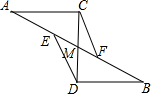 如图,AC=BD,∠A=∠B,点E、F在AB上,且DE∥CF,CD与AB交于点M,小明经过研究发现该图形是中心对称图形,则该图形的对称中心是点M.
如图,AC=BD,∠A=∠B,点E、F在AB上,且DE∥CF,CD与AB交于点M,小明经过研究发现该图形是中心对称图形,则该图形的对称中心是点M.
分析 根据平行线的性质、结合题意证明AM=BM,EM=FM,根据中心对称图形的概念解答即可.
解答 解:∵∠A=∠B,
∴AC∥BD,
∴$\frac{CM}{DM}$=$\frac{AC}{BD}$,又AC=BD,
∴AM=BM,
∵DE∥CF,
∴$\frac{EM}{FM}$=$\frac{CM}{DM}$=1,
∴EM=FM,
∴该图形是中心对称图形,则该图形的对称中心是点M,
故答案为:点M.
点评 本题考查的是中心对称图形,把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
2.从1,3,-4这三个数中,随机抽取两个数相乘,积是正数的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
9.某班实行每周量化考核制,学期末对考核成绩进行统计,结果显示甲、乙两组的平均成绩相同,方差分别是S甲2=36,S乙2=30,则两组成绩的稳定性( )
| A. | 甲组比乙组的成绩稳定 | B. | 乙组比甲组的成绩稳定 | ||
| C. | 甲、乙两组的成绩一样稳定 | D. | 无法确定 |
19.如图是某市某中学八年级(1)班学生参加音乐、美术、体育课外兴趣小组人数的部分条形统计图和扇形统计图,则下列说法错误的是( )
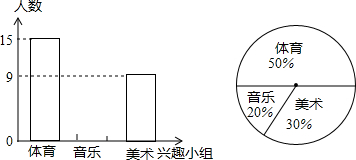

| A. | 八年级(1)班参加这三个课外兴趣小组的学生总人数为30人 | |
| B. | 在扇形统计图中,八年级(1)班参加音乐兴趣小组的学生人数所占的圆心角度数为82° | |
| C. | 八年级(1)班参加音乐兴趣小组的学生人数为6人 | |
| D. | 若该校八年级参加这三个兴趣小组的学生共有200人,那么估计全年级参加美术兴趣小组的学生约有60人 |


 如图,在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,连结AF,CE.求证:四边形AECF是平行四边形.
如图,在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,连结AF,CE.求证:四边形AECF是平行四边形. 如图,直线AB,CD相交于O,射线OM平分∠AOC,若∠BOD=80°,求∠BOM的度数.
如图,直线AB,CD相交于O,射线OM平分∠AOC,若∠BOD=80°,求∠BOM的度数.