题目内容
20. 如图,E为?ABCD外的一点,AE=DE,BE=CE,AE⊥EC,BE⊥ED,四边形ABCD是矩形吗?请证明你的结论.
如图,E为?ABCD外的一点,AE=DE,BE=CE,AE⊥EC,BE⊥ED,四边形ABCD是矩形吗?请证明你的结论.
分析 只要证明△AEC≌△DEB得AC=BD,即可求解.
解答 解:四边形ABCD是矩形.
理由:∵AE⊥EC,BE⊥ED,
∴∠AEC=∠BED=90°,
在△AEC和△DEB中,
$\left\{\begin{array}{l}{AE=DE}\\{∠AEC=∠BED}\\{EC=BE}\end{array}\right.$,
∴△AEC≌△DEB,
∴AC=BD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
点评 本题考查矩形的判定、全等三角形的判定和性质,熟练掌握全矩形的判定方法是解题的关键,记住矩形的三种判定方法:有一个角是直角的平行四边形是矩形,对角线相等的平行四边形是矩形,有三个角是直角的四边形是矩形,属于参考常考题型.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
11.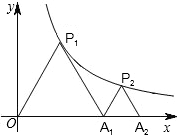 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )| A. | -1+$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | -2+2$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
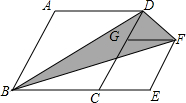 如图,菱形ABCD和菱形CEFG,AB=2,∠A=120°,点G在CD上,点B,C,E在同一条直线上,连接BD,BF,则△BDF的面积为$\sqrt{3}$.
如图,菱形ABCD和菱形CEFG,AB=2,∠A=120°,点G在CD上,点B,C,E在同一条直线上,连接BD,BF,则△BDF的面积为$\sqrt{3}$.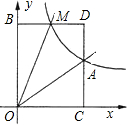 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D. 在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm.
在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm.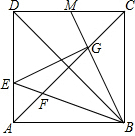 如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.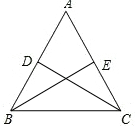 如图,D、E分别是AB、AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E,求证:AC=AB.
如图,D、E分别是AB、AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E,求证:AC=AB.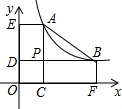 如图,点A,B在双曲线y=$\frac{k}{x}$(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,$\frac{AP}{PC}$=2且△ABP的面积为4,有以下结论:
如图,点A,B在双曲线y=$\frac{k}{x}$(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,$\frac{AP}{PC}$=2且△ABP的面积为4,有以下结论: