题目内容
20.从甲地到乙地有两条公路,一条是全长450公里的普通公路,一条是全长330公里的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快35公里/小时,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半.如果设该客车由高速公路从甲地到乙地所需时间为x小时,那么x满足的分式方程是( )| A. | $\frac{450}{x}$=$\frac{330}{x+35}$×2 | B. | $\frac{450}{x}$=$\frac{330}{2x}$-35 | C. | $\frac{450}{x}$-$\frac{330}{2x}$=35 | D. | $\frac{330}{x}$-$\frac{450}{2x}$=35 |
分析 设出未知数,根据客车在高速公路上行驶的平均速度比在普通公路上快35公里/小时,列出方程即可.
解答 解:设该客车由高速公路从甲地到乙地所需时间为x小时,那么由普通公路从甲地到乙地所需时间为2x,
由题意得,$\frac{330}{x}$-$\frac{450}{2x}$=35,
故选:D.
点评 本题考查的是列分式方程解应用题,正确设出未知数、找出合适的等量关系是解题的关键.

练习册系列答案
相关题目
15.如果不等式2x-m<0只有三个正整数解,那么m的取值范围是( )
| A. | m<8 | B. | m≥6 | C. | 6<m≤8 | D. | 6≤m<8 |
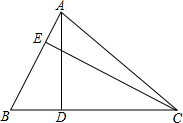 如图,在△ABC中,AB=2,BC=4,△ABC的高AD与CE的比是多少?(提示:利用三角形的面积公式)
如图,在△ABC中,AB=2,BC=4,△ABC的高AD与CE的比是多少?(提示:利用三角形的面积公式)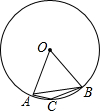 如图,点A,B,C是⊙O上的点,AO=AB,则∠ACB=150度.
如图,点A,B,C是⊙O上的点,AO=AB,则∠ACB=150度.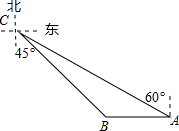 如图,码头A在码头B的正东方向,两个码头之间的距离为32海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.01海里)
如图,码头A在码头B的正东方向,两个码头之间的距离为32海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.01海里)