题目内容
5．
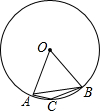如图，点A，B，C是⊙O上的点，AO=AB，则∠ACB=150度．
分析 根据AO=AB，且OA=OB，得出△OAB是等边三角形，再利用圆周角和圆心角的关系得出∠BAC+∠ABC=30°，解答即可．
解答 解：∵点A，B，C是⊙O上的点，AO=AB，
∴OA=OB=AB，
∴△OAB是等边三角形，
∴∠AOB=60°，
∴∠BAC+∠ABC=30°，
∴∠ACB=150°，
故答案为：150
点评 此题考查了圆心角、圆周角定理问题，关键是根据AO=AB，且OA=OB，得出△OAB是等边三角形．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16．
如图，在Rt△ABC中，∠BAC=90°，∠ABC的平分线BD交AC于点D，DE是BC的垂直平分线，点E是垂足．已知DC=8，AD=4，则图中长为4$\sqrt{3}$的线段有（ ）
如图，在Rt△ABC中，∠BAC=90°，∠ABC的平分线BD交AC于点D，DE是BC的垂直平分线，点E是垂足．已知DC=8，AD=4，则图中长为4$\sqrt{3}$的线段有（ ）| A． | 4条 | B． | 3条 | C． | 2条 | D． | 1条 |
20．从甲地到乙地有两条公路，一条是全长450公里的普通公路，一条是全长330公里的高速公路，某客车在高速公路上行驶的平均速度比在普通公路上快35公里/小时，由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半．如果设该客车由高速公路从甲地到乙地所需时间为x小时，那么x满足的分式方程是（ ）
| A． | $\frac{450}{x}$=$\frac{330}{x+35}$×2 | B． | $\frac{450}{x}$=$\frac{330}{2x}$-35 | C． | $\frac{450}{x}$-$\frac{330}{2x}$=35 | D． | $\frac{330}{x}$-$\frac{450}{2x}$=35 |
