题目内容
3. 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
分析 由旋转的性质得出CD=CB,得出∠CDG=∠G,由平行四边形的性质得出∠ADC=∠DCG,证出∠CDG=∠G=∠DCG,得出∠DCG=60°即可.
解答 解:由旋转的性质得:CD=CG,
∴∠CDG=∠G,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AD∥BG,
∴∠ADC=∠DCG,
∵∠ADC=∠G,
∴∠CDG=∠G=∠DCG,
∴∠DCG=60°,
即旋转的角度为60°,
故选:D.
点评 本题考查了旋转的性质和平行四边形的性质;熟练掌握平行四边形的性质和旋转的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.化简($\frac{x}{x-1}$-$\frac{2x+2}{{x}^{2}-1}$)$÷\frac{x-2}{{x}^{2}-x}$的结果是( )
| A. | x | B. | $\frac{1}{x}$ | C. | $\frac{x+1}{x-1}$ | D. | $\frac{x-1}{x+1}$ |
14.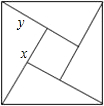 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
11.借助计算器可求得$\sqrt{{4^2}+{3^2}}=5,\sqrt{{{44}^2}+{{33}^2}}=55,\sqrt{{{444}^2}+{{333}^2}}$=555,…,仔细观察上面几道题的计算结果,试猜想$\sqrt{{{\underbrace{44…4}_{2016个}}^2}+{{\underbrace{33…3}_{2016个}}^2}}$=( )
| A. | $\underbrace{55…5}_{2013个}$ | B. | $\underbrace{55…5}_{2014个}$ | C. | $\underbrace{55…5}_{2015个}$ | D. | $\underbrace{55…5}_{2016个}$ |
18.已知一次函数y=kx+b的图象经过点(-2,3),且y的值随x值的增大而增大,则下列判断正确的是( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
15. 一个几何体的三视图如图所示,那么这个几何体的形状是( )
一个几何体的三视图如图所示,那么这个几何体的形状是( )
 一个几何体的三视图如图所示,那么这个几何体的形状是( )
一个几何体的三视图如图所示,那么这个几何体的形状是( )| A. |  | B. |  | C. |  | D. |  |
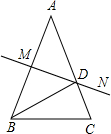 如图,在△ABC中,AB=AC=8,BC=5,∠A=40°,AB边的中垂线MN交AC于点D,交AB于点M.
如图,在△ABC中,AB=AC=8,BC=5,∠A=40°,AB边的中垂线MN交AC于点D,交AB于点M.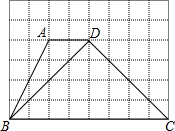 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,连接BD.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,连接BD. 如图,在平面直角坐标系xOy中,直线y=mx+1与双曲y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点D(1,-2),连结OA、OD、DC、AC,四边形AODC为菱形.
如图,在平面直角坐标系xOy中,直线y=mx+1与双曲y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点D(1,-2),连结OA、OD、DC、AC,四边形AODC为菱形.