题目内容
19．如果等式x3•xm=x6成立，那么m=（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 直接利用同底数幂的乘法运算法则得出m的值即可．
解答 解：∵等式x3•xm=x6成立，
∴3+m=6，
解得：m=3．
故选：B．
点评 此题主要考查了同底数幂的乘法运算，正确掌握运算法则是解题关键．
练习册系列答案
相关题目
9．
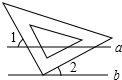如图，已知a∥b，三角板的直角顶点在直线b上，∠1=54°，那么∠2等于（ ）
如图，已知a∥b，三角板的直角顶点在直线b上，∠1=54°，那么∠2等于（ ）| A． | 45° | B． | 36° | C． | 54° | D． | 126° |
10．
已知，△ABC中，AB=AC，BE∥AC，∠BDE=110°，∠BAD=70°，则∠E=（ ）
已知，△ABC中，AB=AC，BE∥AC，∠BDE=110°，∠BAD=70°，则∠E=（ ）| A． | 20° | B． | 30° | C． | 40° | D． | 50° |
用5个完全相同的小正方体组成的如图的立体图形，它的左视图是（ ）
14．
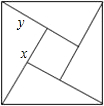如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x、y表示直角三角形的两直角边（x＞y），下列四个说法：①x2+y2=49，②x-y=2，③2xy+4=49，④x+y=9．其中说法正确的是（ ）
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x、y表示直角三角形的两直角边（x＞y），下列四个说法：①x2+y2=49，②x-y=2，③2xy+4=49，④x+y=9．其中说法正确的是（ ）| A． | ①② | B． | ①②③ | C． | ①②④ | D． | ①②③④ |
4．不等式组$\left\{\begin{array}{l}{2x-1＜1}\\{-x≤2}\end{array}\right.$的解集为（ ）
| A． | -2＜x＜1 | B． | x＜1 | C． | -2≤x＜1 | D． | x≥-2 |
11．借助计算器可求得$\sqrt{{4^2}+{3^2}}=5，\sqrt{{{44}^2}+{{33}^2}}=55，\sqrt{{{444}^2}+{{333}^2}}$=555，…，仔细观察上面几道题的计算结果，试猜想$\sqrt{{{\underbrace{44…4}_{2016个}}^2}+{{\underbrace{33…3}_{2016个}}^2}}$=（ ）
| A． | $\underbrace{55…5}_{2013个}$ | B． | $\underbrace{55…5}_{2014个}$ | C． | $\underbrace{55…5}_{2015个}$ | D． | $\underbrace{55…5}_{2016个}$ |
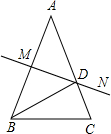如图，在△ABC中，AB=AC=8，BC=5，∠A=40°，AB边的中垂线MN交AC于点D，交AB于点M．
9．
如图，四边形ABCD是正方形，点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合．若∠BAE=40°，则旋转的角度是（ ）
如图，四边形ABCD是正方形，点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合．若∠BAE=40°，则旋转的角度是（ ）| A． | 10° | B． | 15° | C． | 40° | D． | 50° |