题目内容
10.367人中至少有2人生日相同,这是必然事件(选填“随机”或“必然”).分析 根据一年有365天、事件发生的可能性大小判断相应事件的类型即可.
解答 解:367人中至少有2人生日相同是必然事件,
故答案为:必然.
点评 本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
5.有一个三位数8□2,□中的数字由小欣投掷的骰子决定,例如,投出点数为1,则8□2就为812.小欣打算投掷一颗骰子,骰子上标有1~6的点数,若骰子上的每个点数出现的机会相等,则三位数8□2是3的倍数的机率为何?( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{10}$ |
2.下列式子中,正确的是( )
| A. | a2•a3=a6 | B. | (3ab2)3=9a3b6 | C. | (a2b)3÷(-ab)2=a4b | D. | (a-2)2=a2-4 |
19.函数y=$\sqrt{x+1}$中自变量x的取值范围是( )
| A. | x>0 | B. | x≥1 | C. | x>-1 | D. | x≥-1 |
20.下列运算正确的是( )
| A. | 3+$\sqrt{3}$=3$\sqrt{3}$ | B. | $\sqrt{{{(-2)}^2}}$=2 | C. | $\sqrt{50}$=$\sqrt{25+25}$=5+5=10 | D. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ |
 如图,矩形的两条对角线夹角为60°,一条短边为2,则矩形的长边长为2$\sqrt{3}$.
如图,矩形的两条对角线夹角为60°,一条短边为2,则矩形的长边长为2$\sqrt{3}$.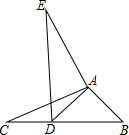 如图,在△ABC中,AB=2,BC=4,∠B=45°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为4-2$\sqrt{2}$.
如图,在△ABC中,AB=2,BC=4,∠B=45°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为4-2$\sqrt{2}$.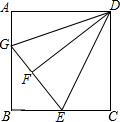 如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.
如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.