题目内容
18.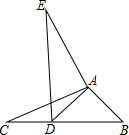 如图,在△ABC中,AB=2,BC=4,∠B=45°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为4-2$\sqrt{2}$.
如图,在△ABC中,AB=2,BC=4,∠B=45°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为4-2$\sqrt{2}$.
分析 依据旋转的性质可得到AD=AB,然后结合∠B=45°可证明△ABD为等腰直角三角形,依据勾股定理可求得BD的长,于是可求得CD的长.
解答 解:∵由旋转的性质可知AD=AB=2,
∴∠B=∠BDA=45°.
∴∠DAB=90°.
∴DB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
∴CD=BC-DB=4-2$\sqrt{2}$.
故答案为:4-2$\sqrt{2}$.
点评 本题主要考查的是旋转的性质、勾股定理的应用,由旋转的性质、等腰三角形的性质以及三角形的内角和定理得到△ABD为等腰直角三角形是解题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
13.2015年12月30日,海南省西环铁路正式投入运营,铁路全长345000米,数据345000用科学记数法表示为( )
| A. | 345×103 | B. | 3.45×105 | C. | 3.45×106 | D. | 3.45×107 |
8.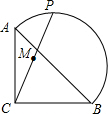 如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
 如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )| A. | $\sqrt{2}$π | B. | π | C. | 2$\sqrt{2}$ | D. | 2 |
