题目内容
20.下列运算正确的是( )| A. | 3+$\sqrt{3}$=3$\sqrt{3}$ | B. | $\sqrt{{{(-2)}^2}}$=2 | C. | $\sqrt{50}$=$\sqrt{25+25}$=5+5=10 | D. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ |
分析 结合选项进行二次根式的化简运算,解答即可.
解答 解:A、3+$\sqrt{3}$≠3$\sqrt{3}$,故本选项错误;
B、$\sqrt{(-2)^{2}}$=$\sqrt{4}$=2,故本选项正确;
C、$\sqrt{50}$=$\sqrt{{5}^{2}×2}$=5$\sqrt{2}$≠10,故本选项错误;
D、$\sqrt{4\frac{1}{9}}$=$\sqrt{\frac{37}{9}}$=$\frac{\sqrt{37}}{3}$≠2$\frac{1}{3}$,故本选项错误.
故选B.
点评 本题考查了二次根式的性质与化简,解答本题的关键在于熟练掌握二次根式的化简.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
11. 如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )
如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )
 如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )
如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{3}}{2}$ | C. | $\sqrt{6}$-$\sqrt{3}$ | D. | 2$\sqrt{3}$-$\sqrt{6}$ |
8.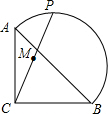 如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
 如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )| A. | $\sqrt{2}$π | B. | π | C. | 2$\sqrt{2}$ | D. | 2 |
12.宽与长的比是$\frac{\sqrt{5}-1}{2}$(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
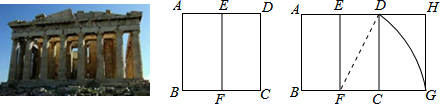

| A. | 矩形ABFE | B. | 矩形EFCD | C. | 矩形EFGH | D. | 矩形DCGH |
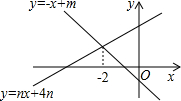 如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )
如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )