Question

15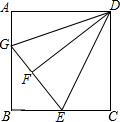．如图，正方形ABCD，AB=10，E为BC的中点，将正方形的边CD沿着DE折叠到DF，延长EF交AB于G，连接DG．
（1）求证：△ADG≌△FDG；
（2）求△BEG的面积．

Answer 1

分析 （1）欲证明△ADG≌△FDG只要证明AD=DF，∠A=∠DFG=90°即可．
（2）设AG=GF=x，在RT△BEG中，由BG²+BE²=GE²列出方程即可求出x，再根据三角形面积公式计算即可．

解答 （1）证明：∵四边形ABCD是正方形，
∴DC=AD，∠C=∠A=90°，
∵△DEF是由△DEC翻折得到，
∴DF=DC，∠DFE=∠DFG=∠C=90°，
∴∠A=∠DFG，AD=DF，
在RT△DGA和RT△DGF中，
$\left\{\begin{array}{l}{DG=DG}\\{DA=DF}\end{array}\right.$，
∴△DGA≌△DGF．
（2）解：∵△DGA≌△DGF，
∴AG=GF，设AG=GF=x，
∵BE=EC=EF=5，
在RT△BEG中，
∵BG²+BE²=GE²，
∴（10-x）²+5²=（x+5）²，
∴x=$\frac{10}{3}$，
∴BG=AB-AG=10-$\frac{10}{3}$=$\frac{20}{3}$
∴S_△BEG=$\frac{1}{2}$×5×$\frac{20}{3}$=$\frac{50}{3}$．

点评 本题考查正方形的性质、全等三角形的判定和性质、翻折变换等知识，解题的关键是熟练掌握全等三角形的判定和性质，学会用方程的思想思考问题，属于中考常考题型．