题目内容
20.若-$\frac{1}{2}$xm+3y与2x4yn+3是同类项,则(m+n)2017=-1.分析 根据同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,可得答案.注意同类项与字母的顺序无关,与系数无关.
解答 解:∵$-\frac{1}{2}{x^{m+3}}y$与2x4yn+3是同类项,
∴m+3=4,n+3=1,
∴m=1,n=-2,
∴(m+n)2017=(1-2)2017=-1,
故答案为:-1.
点评 本题考查同类项的定义,同类项定义中的两个“相同”:所含字母相同;相同字母的指数相同,是易混点,还有注意同类项定义中隐含的两个“无关”:①与字母的顺序无关;②与系数无关.

练习册系列答案
相关题目
10.若$\frac{3-2x}{x-1}$= +$\frac{1}{x-1}$,则 中的数是( )
| A. | -1 | B. | -2 | C. | -3 | D. | 任意实数 |
11.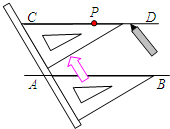 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )| A. | 同位角相等,两直线平行 | |
| B. | 内错角相等,两直线平行 | |
| C. | 同旁内角互补,两直线品行 | |
| D. | 过直线外一点有且只有一条直线与这条直线平行 |
8.与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{\frac{1}{8}}$ | C. | $\sqrt{0.2}$ | D. | $\sqrt{27}$ |
15.下列调查中适合采用普查的是( )
| A. | 调查市场上某种白酒中塑化剂的含量 | |
| B. | 调查鞋厂生产的鞋底能承受的弯折次数 | |
| C. | 了解某火车的一节车厢内感染禽流感病毒的人数 | |
| D. | 了解某城市居民收看江苏卫视的时间 |
5.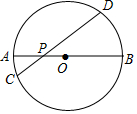 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )| A. | $\sqrt{15}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{15}$ | D. | 8 |
12.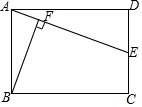 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )| A. | $\frac{3\sqrt{10}}{2}$ | B. | $\frac{3\sqrt{10}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
