题目内容
10．若$\frac{3-2x}{x-1}$= +$\frac{1}{x-1}$，则 中的数是（ ）| A． | -1 | B． | -2 | C． | -3 | D． | 任意实数 |
分析 直接利用分式加减运算法则计算得出答案．
解答 解：∵$\frac{3-2x}{x-1}$= +$\frac{1}{x-1}$，
∴$\frac{3-2x}{x-1}$-$\frac{1}{x-1}$=$\frac{3-2x-1}{x-1}$=$\frac{2-2x}{x-1}$=$\frac{2（1-x）}{x-1}$=-2，
故____中的数是-2．
故选：B．
点评 此题主要考查了分式的加减运算，正确掌握分式加减运算法则是解题关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20．输入一组数据，按下列程序进行计算（x+8）2-826，输出结果如表：
分析表格中的数据，估计方程（x+8）2-826=0的一个正数解x的大致范围为（ ）
| x | 20.5 | 20.6 | 20.7 | 20.8 | 20.9 |
| 输出 | -13.75 | -8.04 | -2.31 | 3.44 | 9.21 |
| A． | 20.5＜x＜20.6 | B． | 20.6＜x＜20.7 | C． | 20.7＜x＜20.8 | D． | 20.8＜x＜20.9 |
1．以下是关于正多边形的描述：
①正多边形的每条边都相等； ②正多边形都是轴对称图形；
③正多边形的外角和是360°；④正多边形都是中心对称图形．
其中正确的描述是（ ）
①正多边形的每条边都相等； ②正多边形都是轴对称图形；
③正多边形的外角和是360°；④正多边形都是中心对称图形．
其中正确的描述是（ ）
| A． | ①②③ | B． | ①②④ | C． | ②③④ | D． | ①②③④ |
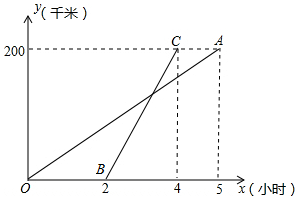甲乙两地相距200千米，一辆货车和一辆轿车先后从甲地出发开往乙地，如图，线段OA表示货车离甲地距离y（千米）与货车行驶时间x（小时）之间的函数关系；线段BC表示轿车离甲地距离y（千米）与货车行驶时间x（小时）的函数关系，请根据图象解答下列问题：
星期日，小英与小平同时从家里出发返回学校，速度分别为3千米/小时，4千米/小时，小平家离学校18千米，小英家在小平返校的路上，离小平家2千米．