题目内容
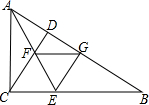 如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.
如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.考点:菱形的判定
专题:证明题
分析:首先利用角平分线的性质证明CE=EG,然后证明△CEF≌△GEF,则FG=FC,根据等角对等边证明CF=CE,从而得到四边形CEGF四边相等,则四边形是菱形.
解答:证明:∵AE平分∠BAC交CD于F,
∴CE=EG,∠AEG=∠AEC,
在△CEF和△GEF中,
,
∴△CEF≌△GEF(SAS),
∴FG=FC,∠CFE=∠GFE,
∵CD⊥AB,EG⊥AB,
∴CD∥EG,
∴∠CFE=∠GEF,
又∵∠CFE=∠GFE,
∴∠CFE=∠CEF,
∴CF=CE,
又∵FG=FC,CE=EG,
∴CF=CE=EG=FG,
∴四边形CEGF是菱形.
∴CE=EG,∠AEG=∠AEC,
在△CEF和△GEF中,
|
∴△CEF≌△GEF(SAS),
∴FG=FC,∠CFE=∠GFE,
∵CD⊥AB,EG⊥AB,
∴CD∥EG,
∴∠CFE=∠GEF,
又∵∠CFE=∠GFE,
∴∠CFE=∠CEF,
∴CF=CE,
又∵FG=FC,CE=EG,
∴CF=CE=EG=FG,
∴四边形CEGF是菱形.
点评:本题考查了平行四边形的性质和判定,菱形的判定,勾股定理,全等三角形的性质和判定的应用,通过做此题培养了学生的推理能力,题目比较好,综合性也比较强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE∥AC交CD的延长线于点E,且∠ACD=∠DBC,S△ADC:S△BED=4:9,AB=10,则AC的长
如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE∥AC交CD的延长线于点E,且∠ACD=∠DBC,S△ADC:S△BED=4:9,AB=10,则AC的长为( )
A、2
| ||
B、2
| ||
| C、6 | ||
D、
|
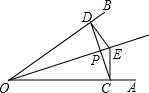 如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论中正确的有( )
如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论中正确的有( )(1)ED=EC;(2)OD=OC;(3)∠ECD=∠EDC;(4)EO平分∠DEC;(5)OE⊥CD;(6)直线OE是线段CD的垂直平分线.
| A、3个 | B、4个 | C、5个 | D、6个 |
 如图,已知AB=AC,以下条件不能得到△ABD≌△ACE的是( )
如图,已知AB=AC,以下条件不能得到△ABD≌△ACE的是( )| A、∠C=∠B |
| B、AD=AE |
| C、BD=CE |
| D、BO=CO |
 平行四边形ABCD中,过A作AE⊥BC,垂足为E,连DE、F为线段DE上一点,且∠1=∠B.求证:△ADF∽△DEC.
平行四边形ABCD中,过A作AE⊥BC,垂足为E,连DE、F为线段DE上一点,且∠1=∠B.求证:△ADF∽△DEC. 如图,为了测量某建筑物的高AB,在距离点B25米的D处安置测角仪,测得点A的仰角α为71°6′,已知仪器的高CD=1.52米,求建筑物的高AB.
如图,为了测量某建筑物的高AB,在距离点B25米的D处安置测角仪,测得点A的仰角α为71°6′,已知仪器的高CD=1.52米,求建筑物的高AB.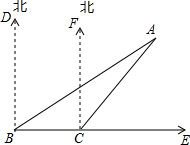 如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?
如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?