题目内容
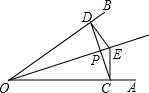 如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论中正确的有( )
如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论中正确的有( )(1)ED=EC;(2)OD=OC;(3)∠ECD=∠EDC;(4)EO平分∠DEC;(5)OE⊥CD;(6)直线OE是线段CD的垂直平分线.
| A、3个 | B、4个 | C、5个 | D、6个 |
考点:角平分线的性质,全等三角形的判定与性质,线段垂直平分线的性质
专题:
分析:根据角平分线上的点到角的两边距离相等可得EC=ED,再利用“HL”证明Rt△OCE和Rt△ODE全等,根据全等三角形对应边相等可得OD=OC,全等三角形对应边相等可∠ECD=∠EDC,再根据等腰三角形三线合一的性质和角平分线的定义解答.
解答:解:∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=ED,故(1)正确;
在Rt△OCE和Rt△ODE中,
,
∴Rt△OCE≌Rt△ODE(HL),
∴OD=OC,∠ECD=∠EDC,故(2)(3)正确;
∴EO平分∠DEC,故(4)正确;
∵OC=OD,OE平分∠AOB,
∴OE⊥CD,故(5)正确;
直线OE是线段CD的垂直平分线,故(6)正确;
综上所述,6个结论都正确.
故选D.
∴EC=ED,故(1)正确;
在Rt△OCE和Rt△ODE中,
|
∴Rt△OCE≌Rt△ODE(HL),
∴OD=OC,∠ECD=∠EDC,故(2)(3)正确;
∴EO平分∠DEC,故(4)正确;
∵OC=OD,OE平分∠AOB,
∴OE⊥CD,故(5)正确;
直线OE是线段CD的垂直平分线,故(6)正确;
综上所述,6个结论都正确.
故选D.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,等腰三角形三线合一的性质以及线段垂直平分线的定义,熟记性质并确定出全等三角形是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
在半径为2cm的⊙O内有长为2
cm的弦AB,由此弦所对的圆心角∠AOB为( )
| 3 |
| A、60° | B、90° |
| C、120° | D、150° |
把代数式“
-5”用文字语言叙述,其中表述不正确的是( )
| 1 |
| x |
| A、比x的倒数小5的数 |
| B、x的倒数与5的差 |
| C、x与5的差的倒数 |
| D、1除以x的商与5的差 |
 如图,A、B两点在数轴上对应的数分别是-20、24,点P、Q两点同时出发,在数轴上运动,它们的速度分别是2个单位/秒、4个单位/秒,它们运动的时间为t秒,当点P、Q在A、B之间相向运动,且满足OP=OQ,则点P对应的数是
如图,A、B两点在数轴上对应的数分别是-20、24,点P、Q两点同时出发,在数轴上运动,它们的速度分别是2个单位/秒、4个单位/秒,它们运动的时间为t秒,当点P、Q在A、B之间相向运动,且满足OP=OQ,则点P对应的数是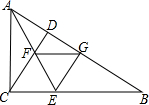 如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.
如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.
 已知点P为⊙O所在平面上一点,过点P的两条直线PA,PC分别交⊙O于A,B和C,D两点,且PO平分∠APC.求证:PA=PC.
已知点P为⊙O所在平面上一点,过点P的两条直线PA,PC分别交⊙O于A,B和C,D两点,且PO平分∠APC.求证:PA=PC. 如图,自行车的两个车轮看作两个圆,则这两个圆的位置关系是
如图,自行车的两个车轮看作两个圆,则这两个圆的位置关系是