题目内容
 如图,已知AB=AC,以下条件不能得到△ABD≌△ACE的是( )
如图,已知AB=AC,以下条件不能得到△ABD≌△ACE的是( )| A、∠C=∠B |
| B、AD=AE |
| C、BD=CE |
| D、BO=CO |
考点:全等三角形的判定
专题:
分析:全等三角形的判定定理有SAS,ASA,AAS,SSS,根据判定定理逐个判断即可.
解答:解:因为∠A=∠A,AB=AC,
A、根据ASA即可推出两三角形全等,故本选项错误;
B、根据SAS即可推出两三角形全等,故本选项错误;
C、不符合全等三角形的判定定理,不能推出两三角形全等,故本选项正确;
D、
连接BC,
∵OB=OC,
∴∠OBC=∠OCB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
再根据ASA即可推出两三角形全等,故本选项错误;
故选C.
A、根据ASA即可推出两三角形全等,故本选项错误;
B、根据SAS即可推出两三角形全等,故本选项错误;
C、不符合全等三角形的判定定理,不能推出两三角形全等,故本选项正确;
D、

连接BC,
∵OB=OC,
∴∠OBC=∠OCB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
再根据ASA即可推出两三角形全等,故本选项错误;
故选C.
点评:本题考查了对全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把代数式“
-5”用文字语言叙述,其中表述不正确的是( )
| 1 |
| x |
| A、比x的倒数小5的数 |
| B、x的倒数与5的差 |
| C、x与5的差的倒数 |
| D、1除以x的商与5的差 |
 如图是个长方形花园,一只小鸟任意落下,掉进花园内,则小鸟在阴影区域内的概率是( )
如图是个长方形花园,一只小鸟任意落下,掉进花园内,则小鸟在阴影区域内的概率是( )A、
| ||
B、
| ||
C、
| ||
| D、不能确定 |
计算:2cos60°+2sin30°+4tan45°=( )
A、2+2
| ||
B、5+
| ||
| C、6 | ||
D、4
|
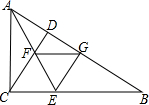 如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.
如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形. 如图,自行车的两个车轮看作两个圆,则这两个圆的位置关系是
如图,自行车的两个车轮看作两个圆,则这两个圆的位置关系是