题目内容
已知x2+x+1=0,求代数式x2006+x2005+x2004+…+x2+x+1的值.
考点:因式分解的应用
专题:
分析:首先把整式x2006+x2005+x2004+…+x2+x+1通过提取公因式,可分解为含有因式1+x+x2的形式.再将1+x+x2的值作为一个整体代入求解.
解答:解:∵1+x+x2+=0,
∴x2006+x2005+x2004+…+x2+x+1
=1+x(1+x+x2)+x5(1+x+x2)+x9(1+x+x2+)+…+x2001(1+x+x2)+x2004(1+x+x2)
=1+(1+x+x2)(x+x5+x9+x12+…+x2001+x2004)
=1+0
=1.
∴x2006+x2005+x2004+…+x2+x+1
=1+x(1+x+x2)+x5(1+x+x2)+x9(1+x+x2+)+…+x2001(1+x+x2)+x2004(1+x+x2)
=1+(1+x+x2)(x+x5+x9+x12+…+x2001+x2004)
=1+0
=1.
点评:此题考查了因式分解的应用;解题的关键是根据已知条件对要求的式子进行因式分解.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
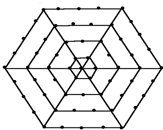 如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推. 如图,A、B两点在数轴上对应的数分别是-20、24,点P、Q两点同时出发,在数轴上运动,它们的速度分别是2个单位/秒、4个单位/秒,它们运动的时间为t秒,当点P、Q在A、B之间相向运动,且满足OP=OQ,则点P对应的数是
如图,A、B两点在数轴上对应的数分别是-20、24,点P、Q两点同时出发,在数轴上运动,它们的速度分别是2个单位/秒、4个单位/秒,它们运动的时间为t秒,当点P、Q在A、B之间相向运动,且满足OP=OQ,则点P对应的数是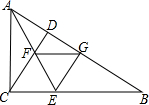 如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.
如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.