题目内容
 如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE∥AC交CD的延长线于点E,且∠ACD=∠DBC,S△ADC:S△BED=4:9,AB=10,则AC的长
如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE∥AC交CD的延长线于点E,且∠ACD=∠DBC,S△ADC:S△BED=4:9,AB=10,则AC的长为( )
A、2
| ||
B、2
| ||
| C、6 | ||
D、
|
考点:相似三角形的判定与性质
专题:
分析:由平行可知△ADC∽△BDE,且S△ADC:S△BED=4:9,可得AD:BD=2:3,且AB=10,可得AD=4,又∠ACD=∠DBC,可证得△ADC∽△ACB,可得AC2=AB•AD,代入可求得AC.
解答:解:∵BE∥AC,
∴△ADC∽△BDE,且S△ADC:S△BED=4:9,
∴AD:BD=2:3,且AB=10,
∴AD=4,
又∵∠ACD=∠DBC,∠A=∠A,
∴△ADC∽△ACB,
∴AC:AB=AD:AC,
∴AC2=AB•AD,
即AC2=10×4=40,
∴AC=2
.
故选B.
∴△ADC∽△BDE,且S△ADC:S△BED=4:9,
∴AD:BD=2:3,且AB=10,
∴AD=4,
又∵∠ACD=∠DBC,∠A=∠A,
∴△ADC∽△ACB,
∴AC:AB=AD:AC,
∴AC2=AB•AD,
即AC2=10×4=40,
∴AC=2
| 10 |
故选B.
点评:本题主要考查相似三角形的判定和性质,由条件求得AD的长,并证明△ADC∽△ACB是解题的关键.

练习册系列答案
相关题目
在半径为2cm的⊙O内有长为2
cm的弦AB,由此弦所对的圆心角∠AOB为( )
| 3 |
| A、60° | B、90° |
| C、120° | D、150° |
 如图是个长方形花园,一只小鸟任意落下,掉进花园内,则小鸟在阴影区域内的概率是( )
如图是个长方形花园,一只小鸟任意落下,掉进花园内,则小鸟在阴影区域内的概率是( )A、
| ||
B、
| ||
C、
| ||
| D、不能确定 |
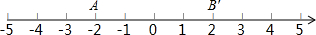
 延长线段AB是指按从端点A到B的方向延长;延长线段BA是指按从端点B到A的方向延长,这时也可以说成反向延长线段AB,如图,分别画出线段AB的延长线和反向延长线.
延长线段AB是指按从端点A到B的方向延长;延长线段BA是指按从端点B到A的方向延长,这时也可以说成反向延长线段AB,如图,分别画出线段AB的延长线和反向延长线. 如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=
如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=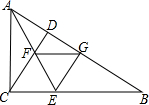 如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.
如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.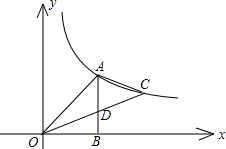 已知:如图,在平面直角坐标系xOy中,直线AC与反比例函数在第一象限内的图象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=
已知:如图,在平面直角坐标系xOy中,直线AC与反比例函数在第一象限内的图象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=