题目内容
7．
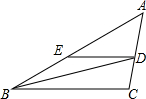BD是△ABC的角平分线，DE∥BC，交AB于点E，∠A=45°，∠BDC=72°，求∠BED的度数．
分析 直接利用三角形外角的性质得出∠ABD的度数，再利用角平分线的性质得出∠DBC的度数，进而利用平行线的性质得出∠BED的度数．
解答 解：∵∠BDC是△ABD的外角，
∴∠ABD=∠BDC-∠A=72°-45°=27°，
∵BD是△ABC的角平分线，
∴∠DBC=∠ABD=27°，
∵DE∥BC，
∴∠BDE=27°，
∴∠BED=180°-∠BDE-∠DBE=180°-27°-27°=126°．
点评 此题主要考查了平行线的性质以及三角形外角以及角平分线的性质，正确得出∠BDE的度数是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=116°，∠ACF=25°，求∠FEC的度数．
12．如果一个△ABC的两个内角A，B分别是67°，46°，则该三角形（ ）
| A． | 不是轴对称图形 | |
| B． | 是轴对称图形，且有三条对称轴 | |
| C． | 是轴对称图形，且对称轴是AC边上的高所在的直线 | |
| D． | 以上答案都不对 |
19．
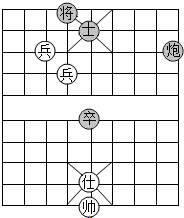如图是中国象棋的一盘残局，如果用（8，7）表示“炮”的位置，用（3，9）表示“将”的位置，那么“帅”的位置应该表示为（ ）
如图是中国象棋的一盘残局，如果用（8，7）表示“炮”的位置，用（3，9）表示“将”的位置，那么“帅”的位置应该表示为（ ）| A． | （8，7） | B． | （0，4） | C． | （0，0） | D． | （4，0） |
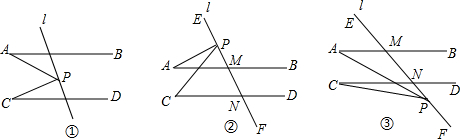
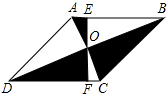如图，在?ABCD中，对角线AC，BD相交于点O，过O作直线交AD于点E，交BC于点F．若?ABCD的面积为30，则阴影部分的面积是15．