题目内容
17. 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数.
分析 由EF与AD平行,AD与BC平行,利用平行于同一条直线的两直线平行得到EF与BC平行,利用两直线平行同旁内角互补求出∠ACB度数,进而求出∠FCB度数,根据CE为角平分线求出∠BCE度数,再利用两直线平行内错角相等即可求出所求角度数.
解答 解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=116°,
∴∠ACB=64°,
又∵∠ACF=25°,
∴∠FCB=∠ACB-∠ACF=39°,
∵CE平分∠BCF,
∴∠BCE=19.5°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=19.5°.
点评 此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.

练习册系列答案
相关题目
7.计算$\sqrt{(-π)^{2}}$的结果是( )
| A. | -π | B. | π | C. | π2 | D. | -π2 |
8.若(x+1)(2x-m)的乘积中不含的一次项,则m的值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
6.如果a∥b,a∥c,那么b与c的位置关系是( )
| A. | 不一定平行 | B. | 一定平行 | C. | 一定不平行 | D. | 以上都有可能 |
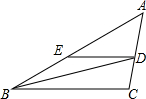 BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=72°,求∠BED的度数.
BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=72°,求∠BED的度数.