题目内容
16.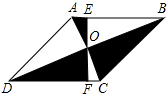 如图,在?ABCD中,对角线AC,BD相交于点O,过O作直线交AD于点E,交BC于点F.若?ABCD的面积为30,则阴影部分的面积是15.
如图,在?ABCD中,对角线AC,BD相交于点O,过O作直线交AD于点E,交BC于点F.若?ABCD的面积为30,则阴影部分的面积是15.
分析 由平行四边形的性质得出OA=OC,AB∥CD,△BCD的面积=$\frac{1}{2}$平行四边形ABCD的面积=15,证出∠AEO=∠CFO,由AAS证明△AOE≌△COF,得出△AOE的面积=△COF的面积,得出阴影部分的面积=△BCD的面积=15即可.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,△BCD的面积=$\frac{1}{2}$平行四边形ABCD的面积=$\frac{1}{2}$×30=15,
∴∠AEO=∠CFO,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠AEO=∠CFO}&{\;}\\{∠AOE=∠COF}&{\;}\\{OA=OC}&{\;}\end{array}\right.$,
∴△AOE≌△COF(AAS),
∴△AOE的面积=△COF的面积,
∴阴影部分的面积=△BCD的面积=15.
故答案为:15.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
6.如果a∥b,a∥c,那么b与c的位置关系是( )
| A. | 不一定平行 | B. | 一定平行 | C. | 一定不平行 | D. | 以上都有可能 |
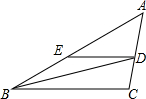 BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=72°,求∠BED的度数.
BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=72°,求∠BED的度数. 在数轴上点A表示的数是$\sqrt{5}$.
在数轴上点A表示的数是$\sqrt{5}$. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形的面积.
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形的面积.