题目内容
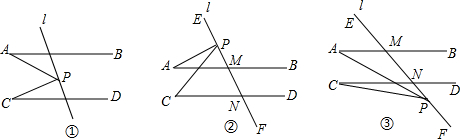
15.已知,AB∥CD,AB,CD被直线l所截,点P是l上的一动点,连接PA,PC.(1)如图①,当P在AB,CD之间时,求证:∠APC=∠A+∠C;
(2)如图②,当P在射线ME上时,探究∠A,∠C,∠APC的关系并证明;
(3)如图③,当P在射线NF上时,直接写出∠A,∠C,∠APC三者之间关系.
分析 (1)过P点作PE∥AB,则∠A=∠APE,再由AB∥CD得出PE∥CD,故∠EPC=∠C,利用等量代换即可得出结论;
(2)先由平行线的性质得出∠C=∠PGM,再由三角形外角的性质即可得出结论;
(3)根据AB∥CD得出∠A=∠AGC,再由三角形外角的性质即可得出结论.
解答 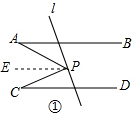 解:(1)如图①,过P点作,PE∥AB,则:∠A=∠APE,
解:(1)如图①,过P点作,PE∥AB,则:∠A=∠APE,
∵AB∥CD,
∴PE∥CD
∴∠EPC=∠C.
又∵∠APC=∠APE+∠EPC,
∴∠APC=∠A+∠C;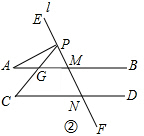
(2)如图②,
∵AB∥CD,
∴∠C=∠PGM.
∵∠PGM=∠A+∠APC,
∴∠C=∠A+∠APC;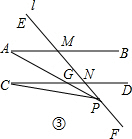
(3)如图③,
∵AB∥CD,
∴∠A=∠AGC.
∵∠AGC=∠C+∠APC,
∴∠A=∠C+∠APC.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
相关题目
6.如果a∥b,a∥c,那么b与c的位置关系是( )
| A. | 不一定平行 | B. | 一定平行 | C. | 一定不平行 | D. | 以上都有可能 |
 如图,在平面直角坐标系中,?ABCD的顶点A(0,0),B(3,0),C(2,2),则顶点D的坐标是(-1,2).
如图,在平面直角坐标系中,?ABCD的顶点A(0,0),B(3,0),C(2,2),则顶点D的坐标是(-1,2).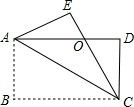 如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.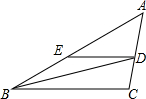 BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=72°,求∠BED的度数.
BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=72°,求∠BED的度数. 在数轴上点A表示的数是$\sqrt{5}$.
在数轴上点A表示的数是$\sqrt{5}$. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形的面积.
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形的面积.