题目内容
15. 如图所示,为了测量某段河面的宽度,李明同学设计了如下测量方案:同学在点A处观测对岸C点,测得∠CAD=45°,又在距A处120m远的B处测得∠CBA=30°,请你根据这些数据算出河宽约为多少?(精确到0.01m,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图所示,为了测量某段河面的宽度,李明同学设计了如下测量方案:同学在点A处观测对岸C点,测得∠CAD=45°,又在距A处120m远的B处测得∠CBA=30°,请你根据这些数据算出河宽约为多少?(精确到0.01m,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
分析 如图所示,CE即为所求线段,而在三角形ACE中,由于∠CAE=45°,则CE=AE,若假设CE=AE=x,则BE=120+x,所以在三角形BCE中tan30°=$\frac{EC}{EB}$,由此可以得到关于x的方程,然后解方程即可.
解答 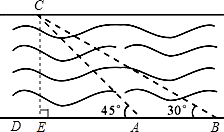 解:过点C作CE⊥BA延长线于点E,
解:过点C作CE⊥BA延长线于点E,
由题意可得:EC=AE,设EC=x,
则tan30°=$\frac{EC}{BE}$=$\frac{x}{x+120}$=$\frac{\sqrt{3}}{3}$,
解得:x=60($\sqrt{3}$+1),
则EC=60($\sqrt{3}$+1)≈163.92(m).
答:河宽约为163.92m.
点评 此题主要考查了三角函数的概念和应用,解题关键是把实际问题转化为数学问题,抽象到三角形中,利用三角函数进行解答.

练习册系列答案
相关题目
5.某商人在一次买卖中均以120元卖出两件商品,其中一件赚了20%,一件赔了20%,在这次交易中,该商人( )
| A. | 不赔不赚 | B. | 赚了10元 | C. | 赔了10元 | D. | 赔了30元 |
6.如图图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.为了保护环境,某企业决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格如′′表:
经预算,该企业购买设备的资金不高于105万元,请你为该企业设计几种购买方案.
| A型 | B型 | |
| 价格(万元/万元) | 12 | 10 |
20.化简:
(1)$\sqrt{4+\sqrt{15}}$
(2)$\sqrt{2-\sqrt{3}}$
(3)$\sqrt{14-3\sqrt{3}}$
(4)$\sqrt{14+5\sqrt{3}}$.
(1)$\sqrt{4+\sqrt{15}}$
(2)$\sqrt{2-\sqrt{3}}$
(3)$\sqrt{14-3\sqrt{3}}$
(4)$\sqrt{14+5\sqrt{3}}$.
7.将式子(a-1)$\sqrt{\frac{1}{1-a}}$中根号外的因式移入根号内的为( )
| A. | $\sqrt{1-a}$ | B. | $\sqrt{a-1}$ | C. | -$\sqrt{1-a}$ | D. | -$\sqrt{a-1}$ |
 已知△ABC中.D、E、F各是三分之一点,确定S△DEF:S△ABC.
已知△ABC中.D、E、F各是三分之一点,确定S△DEF:S△ABC.