题目内容
6.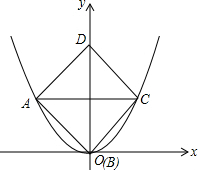 已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.
已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.
分析 由正方形的边长为2,求得对角线AC=2$\sqrt{2}$,则C点坐标为($\sqrt{2}$,$\sqrt{2}$),设此抛物线的解析式为y=ax2,代入点C求得答案即可.
解答 解:∵正方形的边长为2,
∴对角线AC=2$\sqrt{2}$,
∴C点坐标为($\sqrt{2}$,$\sqrt{2}$),
设此抛物线的解析式为y=ax2,
则$\sqrt{2}$=2a,
a=$\frac{\sqrt{2}}{2}$,
抛物线的解析式为y=$\frac{\sqrt{2}}{2}$x2.
故答案为:$\frac{\sqrt{2}}{2}$x2.
点评 此题考查待定系数法求函数解析式,正方形的性质,求得点C或A坐标是解决问题的关键.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
11.已知点C在线段AB的延长线上,5CB=2AC,则$\frac{AC}{AB}$的值是( )
| A. | $\frac{7}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{2}$ | D. | $\frac{5}{2}$ |
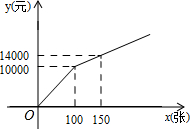 在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案: 已知等腰Rt△ABC,BD是AC边上的中线,∠CBD=∠ACE.求证:∠CDF=∠ADE.
已知等腰Rt△ABC,BD是AC边上的中线,∠CBD=∠ACE.求证:∠CDF=∠ADE.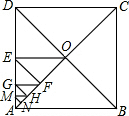 如图,在正方形ABCD中,AO⊥BD、OE、FG、HM都垂直于AD,EF、GH、MN都垂直于AO,如果△AMN的面积为1,那么正方形ABCD的边长等于( )
如图,在正方形ABCD中,AO⊥BD、OE、FG、HM都垂直于AD,EF、GH、MN都垂直于AO,如果△AMN的面积为1,那么正方形ABCD的边长等于( )