题目内容
16.设a<b<c<d,求y=|x-a|+|x-b|+|x-c|+|x-d|的最小值,并求出此时x的取值.分析 本题也可用“零点分段法”讨论计算,但比较麻烦.若能利用|x-a|,|x-b|,|x-c|,|x-d|的几何意义来解题,将显得更加简捷便利.
解答 解:设a,b,c,d,x在数轴上的对应点分别为A,B,C,D,X,
则|x-a|表示线段AX之长,
同理,|x-b|,|x-c|,|x-d|分别表示线段BX,CX,DX之长.
现要求|x-a|,|x-b|,|x-c|,|x-d|之和的值最小,就是要在数轴上找一点X,使该点到A,B,C,D四点距离之和最小.
因为a<b<c<d,
所以A,B,C,D的排列应如图所示:
所以当X在B,C之间,即b<x<c时,距离和最小,这个最小值为AD+BC,
即(d-a)+(c-b).
点评 考查了绝对值,以上分别用两种不同的方法即几何方法和代数方法进行求解.通过比较,可以发现借助数轴用几何方法化简含有绝对值的式子,比较有关数的大小有直观、简捷,举重若轻的优势.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
4. 如图,直角△ABC的周长为24,且AB:AC=5:4,则AC=( )
如图,直角△ABC的周长为24,且AB:AC=5:4,则AC=( )
 如图,直角△ABC的周长为24,且AB:AC=5:4,则AC=( )
如图,直角△ABC的周长为24,且AB:AC=5:4,则AC=( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
11.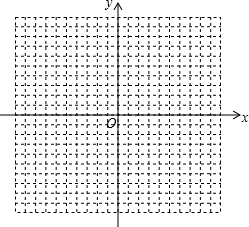 在同一坐标系中画出下列函数的图象:
在同一坐标系中画出下列函数的图象:
(1)y=-x2;
(2)y=-(x+2)2
(3)y=-(x-1)2
 在同一坐标系中画出下列函数的图象:
在同一坐标系中画出下列函数的图象:(1)y=-x2;
(2)y=-(x+2)2
(3)y=-(x-1)2
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=-x2 | … | … | |||||||||
| y=-(x+2)2 | … | … | |||||||||
| y=-(x-1)2 | … | … |
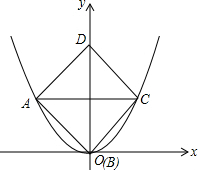 已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.
已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.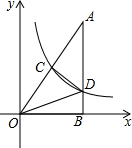 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=18,则S△OBD的值为12.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=18,则S△OBD的值为12. 如图,已知∠1=65°,∠2=115°.直线BC与DF平行吗?为什么?
如图,已知∠1=65°,∠2=115°.直线BC与DF平行吗?为什么?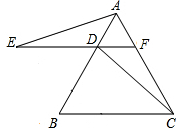 如图,△ABC是等边三角形,过AB上的一点D作DF∥BC,交AC于F,在FD的延长线上取点E,使DE=DB,连接AE、CD.证明:△AFE≌△DAC.
如图,△ABC是等边三角形,过AB上的一点D作DF∥BC,交AC于F,在FD的延长线上取点E,使DE=DB,连接AE、CD.证明:△AFE≌△DAC.