题目内容
17. 在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)
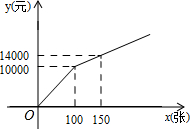
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为y=50x+10000;方案二中,当0≤x≤100时,y与x的函数关系式为y=100x,当x>100时,y与x的函数关系式为y=80x+2000;
(2)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共600张,花去总费用计48000元,求甲、乙两单位各购买门票多少张.
分析 (1)依题意可得方案一:y与x的函数关系式y=50x+10000;方案二考查了分段函数的有关知识(0≤x≤100;x>100),利用待定系数法即可解答;
(2)设设甲购买门票m张,则乙购买门票(600-m)张.,分别可采用方案一或方案二购买.
解答 解:(1)由题意得,方案一中,y与x的函数关系式为:y=50x+10000,
方案二:当0≤x≤100时,y=100x,
当x>100时,设y与x之间的函数关系式为y=kx+b,
把(100,10000),(150,14000)代入得:$\left\{\begin{array}{l}{100k+b=10000}\\{150k+b=14000}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=80}\\{b=2000}\end{array}\right.$,
则y=80x+2000,
故答案为:y=50x+10000,y=100x,y=80x+2000.
(2)设甲购买门票m张,则乙购买门票(600-m)张.
①当0≤600-m≤100时,10000+500m+100(600-m)=48000
10000+500m+60000-100m=48000
-50m=-22000
m=440,
∵600-m=160>100,
∴此法舍去
②当600-m>100时,10000+50m+80(600-m)+2000=48000
10000+50m+48000-80m+2000=48000
-30m=-1200
m=400,
600-m=200>100.
答:甲单位购买门票400张,乙单位购买门票200张.
点评 本题考查了一次函数的应用,解决本题的关键是利用待定系数法确定一次函数的解析式,在(2)中注意分类讨论思想的应用.

 将一副三角板按如图所示方式放置,则∠1与∠2的和是( )
将一副三角板按如图所示方式放置,则∠1与∠2的和是( )| A. | 60° | B. | 45° | C. | 30° | D. | 25° |
| A. | 12.56×104元 | B. | 1.256×105元 | C. | 1.256×104元 | D. | 1256×106元 |

| A. | 4017 | B. | 4018 | C. | 4019 | D. | 4020 |
 关于x的不等式x-3>$\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是-12.
关于x的不等式x-3>$\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是-12. 在△ABC中,总有$\frac{AB}{sinC}$=$\frac{AC}{sinB}$=$\frac{BC}{sinA}$,利用这个知识请解答下题:
在△ABC中,总有$\frac{AB}{sinC}$=$\frac{AC}{sinB}$=$\frac{BC}{sinA}$,利用这个知识请解答下题: 如图,∠A0B=60°,点P在0A上,点M、N在OB上,PM=PN,若OP=10,OM=4,则MN的长为( )
如图,∠A0B=60°,点P在0A上,点M、N在OB上,PM=PN,若OP=10,OM=4,则MN的长为( )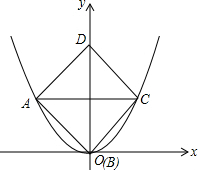 已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.
已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.