题目内容
6.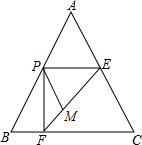 如图,在△ABC中,AB=AC=2$\sqrt{5}$,BC=4,P是AB边上的动点(不与A,B重合),过P作PE∥BC交AC于E,作PF⊥BC,垂足为F,连接EF,M是EF上的点,且EM=2FM,设BF=m.
如图,在△ABC中,AB=AC=2$\sqrt{5}$,BC=4,P是AB边上的动点(不与A,B重合),过P作PE∥BC交AC于E,作PF⊥BC,垂足为F,连接EF,M是EF上的点,且EM=2FM,设BF=m.(1)直接写出△EMP与△FMP的面积的数量关系;
(2)①求PE,PF的长(分别用含m的代数式表示);
②设△PEM的面积为S,求S与m的函数关系式,并求S的最大值;
③△PEM能否成为等腰三角形?若能,求出相应的m的值;若不能,请说明理由;
(3)直接写出PM长度的最小值.
分析 (1)如图1,过点P作PK⊥EF,垂足为K.,根据三角形的面积公式可知:${S}_{△EMP}=\frac{1}{2}EM•PK$,${S}_{△PMF}=\frac{1}{2}FM•PK$,又因为EM=2FM,故此S△EMP=2S△PMF;
(2)①过点A作AG⊥BC于G,交PE于H,则BG=GC=2,AG=4,由PF∥AG,得$\frac{BF}{BG}=\frac{PF}{AG}$,可知PF=2m,由PE∥BC得$\frac{PE}{BC}=\frac{AH}{AG}$,可知:PE=4-2m;②S=$\frac{2}{3}{S}_{△PEF}=\frac{2}{3}×\frac{1}{2}•2m•(4-2m)$=-$\frac{4}{3}(m-1)^{2}+\frac{4}{3}$,利用二次函数的性质求得最值即可;③能成为等腰三角形.当PM=ME时,则M为EF的中点,与已知ME=2MF矛盾;当PE=ME,则$\frac{PE}{EF}=\frac{2}{3}$,所以$\frac{PE}{PF}=\frac{2}{\sqrt{5}}$,可求得m=10-4$\sqrt{5}$;若PM=ME,过点P作PK⊥EF与K,则K为ME的中点,故此$\frac{EK}{FK}=\frac{1}{2}$.,由相似三角形的面积比等于相似比的平方得:$(\frac{PE}{PF})^{2}=\frac{1}{2}$,即:$(\frac{4-2m}{2m})^{2}=\frac{1}{2}$,解得m=4-2$\sqrt{2}$,综上所述可求得△PEM为等腰三角形时m的值;
(3)如图3所示:过点A作AG⊥BC于G,交PE于H,连接PG,首先证明点P、M、G在一条直线上,然后由PE∥FG,可知$\frac{PM}{PG}=\frac{2}{3}$,即PM=$\frac{2}{3}$PG,故此当GP⊥AB时,PM有最小值,先证明△PBG∽△GBA,从而可求得PG=$\frac{4\sqrt{5}}{5}$,所以PM=$\frac{8\sqrt{5}}{15}$.
解答 解:(1)如图1,过点P作PK⊥EF,垂足为K.
${S}_{△EMP}=\frac{1}{2}EM•PK$,${S}_{△PMF}=\frac{1}{2}FM•PK$,
又∵EM=2FM.
∴S△EMP=2S△PMF;
(2)如图2所示.
①过点A作AG⊥BC于G,交PE于H,则BG=GC=2,AG=$\sqrt{(2\sqrt{5})^{2}-{2}^{2}}=4$.
由PF∥AG,得$\frac{BF}{BG}=\frac{PF}{AG}$,
∴$\frac{m}{2}=\frac{PF}{4}$.
∴PF=2m.
由PE∥BC得$\frac{PE}{BC}=\frac{AH}{AG}$,
∴$\frac{PE}{4}=\frac{4-2m}{4}$.
∴PE=4-2m.
②∵EM=2FM,
∴S△EMP=2S△PMF.
∴S=$\frac{2}{3}{S}_{△PEF}=\frac{2}{3}×\frac{1}{2}•2m•(4-2m)$=-$\frac{4}{3}(m-1)^{2}+\frac{4}{3}$.
∵$-\frac{4}{3}<0$,
∴S有最大值,最大值为$\frac{4}{3}$.
③能成为等腰三角形.
当PM=ME时,则M为EF的中点,与已知ME=2MF矛盾;
若PE=ME,则$\frac{PE}{EF}=\frac{2}{3}$,
∴$\frac{PE}{PF}=\frac{2}{\sqrt{5}}$,即$\frac{4-2m}{2m}=\frac{2}{\sqrt{5}}$.
解得:m=10-4$\sqrt{5}$.
若PM=PE,过点P作PK⊥EF与K,则K为ME的中点,
∴$\frac{EK}{FK}=\frac{1}{2}$.
∵△PFK∽△EPK,由相似三角形的面积比等于相似比的平方得:$(\frac{PE}{PF})^{2}=\frac{1}{2}$,即:$(\frac{4-2m}{2m})^{2}=\frac{1}{2}$,
∴m=4-2$\sqrt{2}$或m=4+2$\sqrt{2}$.
∵BC=4,
∴m≤4.
∴m=4-2$\sqrt{2}$.
综上所述,当m=10-4$\sqrt{5}$或m=4-2$\sqrt{2}$时,△PEM为等腰三角形;
(3)如图3所示:过点A作AG⊥BC于G,交PE于H,连接PG.
∵PE∥BC,AG⊥BC,
∴AG⊥PE.
∴∠PHG=90°.
∴∠HGP+∠HPG=90°.
∵AG⊥BC,PF⊥BC,
∴PF∥AG.
∴∠HGP=∠GPF.
∴∠HPG+∠GPG=90°.
又∵∠HPG+MPF=90°,
∴∠MPF=∠GPF.
∴点P、M、G在一条直线上.
∵PE∥FG,
∴$\frac{PM}{MG}=\frac{ME}{FM}=\frac{2}{1}$.
∴$\frac{PM}{PG}=\frac{2}{3}$,即PM=$\frac{2}{3}$PG.
∴当GP⊥AB时,PG有最小值,即PM有最小值.
∵∠B=∠B,∠BGA=∠BPG,
∴△PBG∽△GBA.
∴$\frac{PG}{BG}=\frac{AG}{AB}$,即$\frac{PG}{2}=\frac{4}{2\sqrt{5}}$.
∴PG=$\frac{4\sqrt{5}}{5}$.
∴PM=$\frac{8\sqrt{5}}{15}$.
点评 本题主要考查的是相似三角形的性质和判定、勾股定理、垂线段最短、平行线的性质和判定、二次函数的最值问题的综合应用,证得点P、M、G在一条直线上是解题的关键.

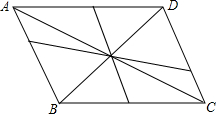 如图,直线BD可以将平行四边形ABCD分成全等的两部分,这样的直线还有很多.
如图,直线BD可以将平行四边形ABCD分成全等的两部分,这样的直线还有很多.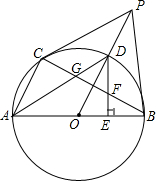 如图,AB为⊙O的直径,PB为⊙O的切线,AC∥OP,点C在⊙O上,OP交⊙O于D,DA交BC于G.
如图,AB为⊙O的直径,PB为⊙O的切线,AC∥OP,点C在⊙O上,OP交⊙O于D,DA交BC于G.