题目内容
17.观察下列等式:$\frac{1}{\sqrt{2}+1}$=$\frac{(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1;
$\frac{1}{\sqrt{3}+\sqrt{2}}=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}-\sqrt{2}$;
$\frac{1}{\sqrt{4}+\sqrt{3}}=\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\sqrt{4}-\sqrt{3}$;…
回答下列问题:
(1)利用你观察到的规律,化简:$\frac{1}{3\sqrt{2}+\sqrt{17}}$;
(2)计算:$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+2}$…+$\frac{1}{\sqrt{15}+4}$.
分析 (1)根据已知的3个等式发现规律:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$,把n=22代入即可求解;
(2)先利用上题的规律将每一个分数化为两个二次根式的差的形式,再计算即可.
解答 解:(1)$\frac{1}{3\sqrt{2}+\sqrt{17}}$=3$\sqrt{2}$-$\sqrt{17}$;
(2)$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+2}$…+$\frac{1}{\sqrt{15}+4}$,
=$\sqrt{2}$-1+$\sqrt{3}-\sqrt{2}$+$\sqrt{4}-\sqrt{3}$…+4-$\sqrt{15}$,
=$\sqrt{15}$-1.
点评 此题考查了分母有理化,得出规律:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
18.如果把分式$\frac{2x}{x-y}$中的x,y都扩大3倍,分式的值( )
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 缩小6倍 |
9. 如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
 如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )| A. | 4 | B. | $\frac{4}{3}$$\sqrt{3}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{8}{3}$$\sqrt{3}$ |
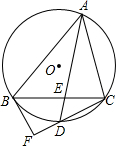 如图,已知⊙O内接△ABC,D为$\widehat{BC}$中点,AD交BC于E点,过B作⊙O的切线交CD延长线于F点,AE=3,DE=1,BF=$\sqrt{15}$,求CF的长.
如图,已知⊙O内接△ABC,D为$\widehat{BC}$中点,AD交BC于E点,过B作⊙O的切线交CD延长线于F点,AE=3,DE=1,BF=$\sqrt{15}$,求CF的长.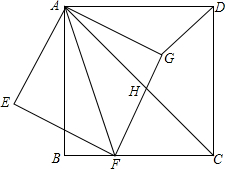 如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.
如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.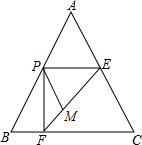 如图,在△ABC中,AB=AC=2$\sqrt{5}$,BC=4,P是AB边上的动点(不与A,B重合),过P作PE∥BC交AC于E,作PF⊥BC,垂足为F,连接EF,M是EF上的点,且EM=2FM,设BF=m.
如图,在△ABC中,AB=AC=2$\sqrt{5}$,BC=4,P是AB边上的动点(不与A,B重合),过P作PE∥BC交AC于E,作PF⊥BC,垂足为F,连接EF,M是EF上的点,且EM=2FM,设BF=m.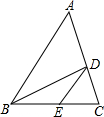 如图,△ABC中,CE:EB=2:3,DE∥AB,若△ABC的面积为25,则△BDE的面积为6.
如图,△ABC中,CE:EB=2:3,DE∥AB,若△ABC的面积为25,则△BDE的面积为6.