题目内容
20．如图a是长方形纸带，∠DEF=26°，将纸带沿EF折叠成图b，则∠FGD的度数是52度，再沿BF折叠成图c，则图c中的∠DHF的度数是78°．
分析 根据两条直线平行，内错角相等，则∠BFE=∠DEF=26°，由三角形的外角性质得出∠FGD的度数；根据平角定义、折叠的性质求出∠CFE=102°，再根据平行线的性质即可求解．
解答 解：
∵AD∥BC，∠DEF=26°，
∴∠BFE=∠DEF=26°，
∴图b中，∠FGD=26°+26°=52°；
图c中，∠CFE=180°-3×26°=102°，
∴∠DHF=180°-102°=78°．
故答案为：52，78°．
点评 本题考查了翻折变换的性质，平行线的性质，三角形的外角性质；熟练掌握翻折变换的性质和平行线的性质是解决问题的关键．
练习册系列答案
相关题目
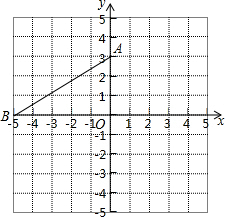如图，在平面直角坐标系中，点A的坐标是（0，3），点B在x轴的负半轴上，将△AOB绕点A逆时针旋转90°得到△AEF，点O，B的对应点分别为E，F．
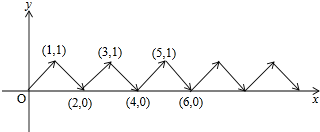如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，1），…，按这样的运动规律，经过第2016次运动后，点P运动的总长度是2016$\sqrt{2}$．
15．化简$\sqrt{16}$得（ ）
| A． | ±4 | B． | ±2 | C． | 4 | D． | -4 |
5．
如图，将矩形ABCD沿AE对折，使点D落在点F处，若∠CEF=60°，则∠EAF等于（ ）
如图，将矩形ABCD沿AE对折，使点D落在点F处，若∠CEF=60°，则∠EAF等于（ ）| A． | 60° | B． | 50° | C． | 40° | D． | 30° |
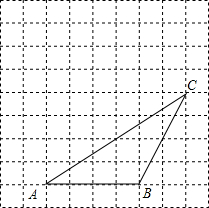如图，网格中每个小正方形边长为1，△ABC的顶点都在格点上．将△ABC向左平移2格，再向上平移3格，得到△A′B′C′．