题目内容
10．已知y=$\sqrt{1-8x}+\sqrt{8x-1}$+2，求$\sqrt{\frac{x}{y}}$+$\sqrt{\frac{y}{x}}$-2的值．分析 由二次根式有意义的条件可知1-8x=0，从而可求得x、y的值，然后将x、y的值代入计算即可．
解答 解：由二次根式有意义的条件可知：1-8x=0，
解得：x=$\frac{1}{8}$．
当x=$\frac{1}{8}$，y=2时，原式=$\sqrt{\frac{1}{16}}+\sqrt{16}$=-2=$\frac{1}{4}$+4-2=2$\frac{1}{4}$．
点评 本题主要考查的是二次根式有意义的条件，掌握二次根式的被开方数大于等于零是解题的关键．
练习册系列答案
相关题目
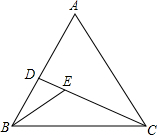如图，在等边△ABC中，D在边AB上，E在CD上，∠BED=60°，DE=2，△ACD的面积6$\sqrt{3}$，则线段CD的长为6．
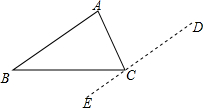请根据图给出的图示（过点C作ED∥AB），对“三角形内角和等于180°”说理．（作平行线是把角从一个位置“转移”到另一个位置的重要手段）
如图，在三角形ABC中，点D、E、F分别是三条边上的点，EF∥AC，DF∥AB，∠B=35°，∠C=65°，则∠EFD=80°．