题目内容
已知平行四边形ABCD,点E是AB的中点,在AD上截取AF=2FD,EF交AC于G,则AG:GC= .
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:过E点作EO∥AF交AC于O,则点O为AC的中点,根据中位线性质有OE=
BC,易得OE═
AD,而AF=2FD,即AF=
AD,于是有OE=
AF,由OE∥AF,根据相似三角形的判定得到△GAF∽△GOE,则
=
=
,即可得
=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| AG |
| GO |
| AF |
| EO |
| 4 |
| 3 |
| AG |
| GC |
| 2 |
| 5 |
解答:解:如图所示,过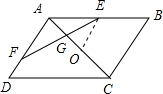 E点作EO∥AF交AC于O,
E点作EO∥AF交AC于O,
∵点E是AB的中点,
∴点O为AC的中点,
∴OE=
BC,
∵四边形ABCD为平行四边形,
∴AD=BC,
∴OE=
AD
∵AF=2FD,
∴AF=
AD,
∴OE=
AF,
∵OE∥AF,
∴△GAF∽△GOE,
∴
=
=
,
∴
=
=
;
故答案为:2:5.
 E点作EO∥AF交AC于O,
E点作EO∥AF交AC于O,∵点E是AB的中点,
∴点O为AC的中点,
∴OE=
| 1 |
| 2 |
∵四边形ABCD为平行四边形,
∴AD=BC,
∴OE=
| 1 |
| 2 |
∵AF=2FD,
∴AF=
| 2 |
| 3 |
∴OE=
| 3 |
| 4 |
∵OE∥AF,
∴△GAF∽△GOE,
∴
| AG |
| GO |
| AF |
| EO |
| 4 |
| 3 |
∴
| AG |
| GC |
| 4 |
| 3+3+4 |
| 2 |
| 5 |
故答案为:2:5.
点评:本题考查了平行线分线段成比例定理:两条直线被一组平行线所截,截得的线段对应成比例.也考查了平行四边形的性质以及相似三角形的判定与性质.

练习册系列答案
相关题目
 如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=8,则PD=( )
如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=8,则PD=( )| A、3 | B、4 | C、5 | D、6 |
已知方程组
的解为
,则a-b的值为( )
|
|
| A、10 | ||
B、
| ||
C、-
| ||
| D、-10 |
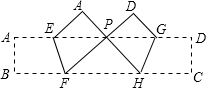 把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?
把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少? 某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m.
某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m.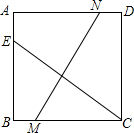 已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数.
已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数.