题目内容
已知2s2+4s-7=0,7t2-4t-2=0,s,t为实数,且st≠1.则
的值为 .
| 3st-2s+3 |
| t |
考点:根与系数的关系
专题:
分析:根据题意可知s与
是方程2x2+4x-7=0的两个根,由根与系数的关系分别求出两根的和与两根的积,代入代数式即可求出代数式的值.
| 1 |
| t |
解答:解:7t2-4t-2=0两边都除以-t2,得
+
-7=0,
即2(
)2+4(
)-7=0,
又∵2s2+4s-7=0,
∴s与
是方程2x2+4x-7=0的两个根,
由韦达定理,得
s+
=-2,s•
=-
,
∴
=3s-2
+
=3(s+
)-2s•
=3×(-2)-2×(-
)
=-6+7
=1.
故答案为1.
| 2 |
| t2 |
| 4 |
| t |
即2(
| 1 |
| t |
| 1 |
| t |
又∵2s2+4s-7=0,
∴s与
| 1 |
| t |
由韦达定理,得
s+
| 1 |
| t |
| 1 |
| t |
| 7 |
| 2 |
∴
| 3st-2s+3 |
| t |
=3s-2
| s |
| t |
| 3 |
| t |
=3(s+
| 1 |
| t |
| 1 |
| t |
=3×(-2)-2×(-
| 7 |
| 2 |
=-6+7
=1.
故答案为1.
点评:本题主要考查的是一元二次方程根与系数的关系及代数式求值.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.
| A、① | B、①② |
| C、①②③ | D、都不正确 |
甲县、乙县各有钢铁100吨,丙地、丁地分别需要钢铁80吨、110吨,研究决定把甲县的100吨运往丙、丁两地,不够的再从乙县补充.实际运好以后,发现从乙县运往丁地x吨,那么从甲县运往丙地( )
| A、(110-x)吨 |
| B、(100-x)吨 |
| C、(x-20)吨 |
| D、(x-10)吨 |
不等式组
的解集为( )
|
| A、x>3 | ||
B、x>
| ||
| C、x<3 | ||
D、
|
 如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处.已知CE=3cm,AB=8cm. 求:
如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处.已知CE=3cm,AB=8cm. 求: 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,且DE=5cm,求BC的长.
如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,且DE=5cm,求BC的长.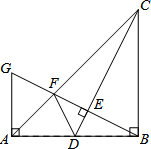 如图:在Rt三角形ABC中,∠ABC=90,BA=BC.点D是AB的中点,连接 CD,过点B作BC作垂直CD,分别交CD、CA于点E、F.与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:(1)
如图:在Rt三角形ABC中,∠ABC=90,BA=BC.点D是AB的中点,连接 CD,过点B作BC作垂直CD,分别交CD、CA于点E、F.与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:(1)