题目内容
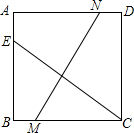已知：如图，正方形ABCD中，点E、M、N分别在AB、BC、AD边上，CE=MN，∠MCE=35°，求∠ANM的度数．考点：正方形的性质
专题：
分析：过M作MG∥AB交AD于G，可证明△GMN≌△BCE，可得到∠ANM=∠CEB，在Rt△BEC中可求得∠CEB，可求得答案．
解答：
解：如图，过M作MG∥AB交AD于G，
∵四边形ABCD为正方形，
∴∠NGN=∠A=∠B=90°，且AB=MG=CD，
在Rt△GMN和Rt△BCE中
∴△GMN≌△BCE（HL），
∴∠ANM=∠CEB，
又∵∠MCE=35°，
∴∠CEB=90°-35°=55°°，
∴∠ANM=55°．
解：如图，过M作MG∥AB交AD于G，∵四边形ABCD为正方形，
∴∠NGN=∠A=∠B=90°，且AB=MG=CD，
在Rt△GMN和Rt△BCE中
|
∴△GMN≌△BCE（HL），
∴∠ANM=∠CEB，
又∵∠MCE=35°，
∴∠CEB=90°-35°=55°°，
∴∠ANM=55°．
点评：本题主要考查正方形的性质及全等三角形的判定和性质，构造三角形全等是解题的关键．
练习册系列答案
相关题目
如图，在△AOB中，∠AOB=90°，AO=3，BO=6，将△AOB绕顶点O逆时针旋转到△A′OB′的位置．若此时线段A′B′与BO的交点C是BO的中点，则线段B′C的长度为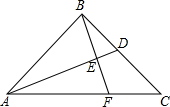
如图，在Rt△ABC中，∠ABC=90°，BA=BC，点D为BC边的中点，BE⊥AD于点E，交AC于点F，求
如图，四边形ABCD和四边形AEFG是正方形，△AED是等边三角形，则图中度数为30°的角有（ ）| A、2个 | B、3个 | C、4个 | D、5个 |
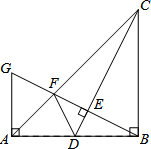如图：在Rt三角形ABC中，∠ABC=90，BA=BC．点D是AB的中点，连接 CD，过点B作BC作垂直CD，分别交CD、CA于点E、F．与过点A且垂直于AB的直线相交于点G，连结DF，给出以下四个结论：（1）
如图，△ABC中，点D在AB上，点E在AC上，添加一个条件（只写出一种情况），使得△ABC∽△AED并给出你的证明过程．
如图，在△ABC中，D为BC上一点，BD=CD，AD⊥AC于点A，∠BAD=30°．