题目内容
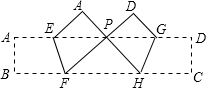把长方形纸条ABCD沿EF，GH同时折叠，B、C两点恰好都落在AD边的P点处，若∠FPH=90°，PF=8，PH=6，则长方形ABCD的面积为多少？考点：翻折变换（折叠问题）
专题：
分析：如图，作辅助线；运用勾股定理求出FH；进而求出PM；求出BC的长度，即可解决问题．
解答：
解：作PM⊥BC于M．
∵∠FPH=90°，PF=8，PH=6，
∴FH=10，AB=PM=
=4.8；
由题意得：BF=PF、GH=PH，
∴BC=PF+PH+FH=24，
∴矩形ABCD的面积=AB•BC=115.2．
解：作PM⊥BC于M．∵∠FPH=90°，PF=8，PH=6，
∴FH=10，AB=PM=
| PF•PH |
| FH |
由题意得：BF=PF、GH=PH，
∴BC=PF+PH+FH=24，
∴矩形ABCD的面积=AB•BC=115.2．
点评：该题主要考查了翻折变换的性质、矩形的性质、勾股定理等几何知识点及其应用问题；解题的关键是作辅助线，灵活运用勾股定理等知识点来分析、推理、解答．
练习册系列答案
相关题目
已知抛物线y=-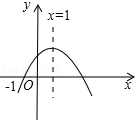
二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①2a+b=0，②4a-2b+c＜0，③ac＞0，④当-1＜x＜3时，y＞0，⑤当x≥1时，y随x的增大而增大，正确结论的序号是
八年级（5）班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．小明同学在制作手工作品的第一、二个步骤是：①先裁下了一张长BC=20cm，宽AB=16cm的长方形纸片ABCD，②将纸片沿着直线AE折叠，点D恰好落在BC边上的点F处，…请你根据①②步骤解答下列问题：
如图，将长方形ABCD沿直线AE折叠，顶点D恰好落在BC边上点F处．已知CE=3cm，AB=8cm． 求：