题目内容
4.某粮食加工厂从生产的粮食中抽出20袋检查质量,以每袋50千克为标准,将超过的千克数记为正数,不足的千克数记为负数,结果记录如下:| 与标准质量的偏差/千克 | -0.7 | -0.5 | -0.2 | 0 | +0.4 | +0.5 | +0.7 |
| 袋数 | 1 | 3 | 4 | 5 | 3 | 3 | 1 |
(1)这20袋大米共超重或不足多少千克?
(2)这20袋大米的总质量为多少千克?平均每袋是多少千克?
分析 (1)根据题目中给出的信息和表格,可以算出这20袋大米实际质量与标准质量的偏差之和与0比较,可得是否超重或不足.
(2)根据第一问中的超重还是不足,再根据标准质量,可以算出这20袋大米的实际质量,从而算出20袋大米的总质量和平均每袋的质量.
解答 解:(1)(-0.7)×1+(-0.5)×3+(-0.2)×4+0×5+0.4×3+0.5×3+0.7×1
=(-0.7)+(-1.5)+(-0.8)+0+1.2+1.5+0.7
=0.4>0.
故这20袋大米共超重0.4千克.
(2)20×50+0.4
=1000+0.4
=1000.4(千克).
1000.4÷20=50.02(千克).
故这20袋大米的总质量为1000.4千克,平均每袋是50.02千克.
故答案为:(1)这20袋大米共超重0.4千克.
(2)这20袋大米的总质量为1000.4千克,平均每袋是50.02千克.
点评 本题考查正数和负数的加法和乘除法,关键是注意表格中的数据的处理,尤其是袋数要注意.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
19.把-(x-y)-z去括号得( )
| A. | -x+y-z | B. | -x-y-z | C. | -x+y+z | D. | -x-y+z |
14.计算$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}y+x{y}^{2}}$$•\frac{xy}{x-y}$的结果为( )
| A. | $\frac{x-y}{x+y}$ | B. | $\frac{x+y}{x-y}$ | C. | $\frac{(x-y)^{2}}{x+y}$ | D. | 1 |
 如图所示,l1∥l2∥l3,$\frac{AB}{BC}$=$\frac{4}{3}$,DE=6,求DF的长.
如图所示,l1∥l2∥l3,$\frac{AB}{BC}$=$\frac{4}{3}$,DE=6,求DF的长.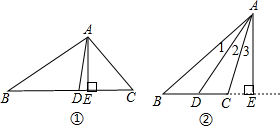 求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.
求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.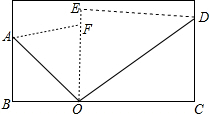 将一张矩形纸片按如图方式折叠,设O点是矩形边上一点,将矩形的一角沿OA翻折使OB与OF重合,再将其邻角沿0D翻折,使OC与OE重合,且O、E、F在同一直线上.求OA与∠BOF、OD与∠EOC的关系.
将一张矩形纸片按如图方式折叠,设O点是矩形边上一点,将矩形的一角沿OA翻折使OB与OF重合,再将其邻角沿0D翻折,使OC与OE重合,且O、E、F在同一直线上.求OA与∠BOF、OD与∠EOC的关系.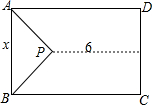 如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.
如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.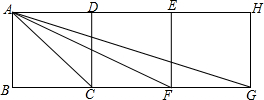 如图,四边形ABCD,CDEF,EFGH均是正方形,且B,C,F,G在一直线上,连接AC,AF,AG
如图,四边形ABCD,CDEF,EFGH均是正方形,且B,C,F,G在一直线上,连接AC,AF,AG