题目内容
12.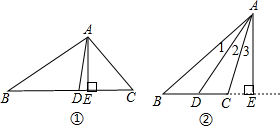 求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.
求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.已知:△ABC中,AE⊥BC于E,AD平分∠BAC,∠C>∠B
求证:∠DAE=$\frac{1}{2}$(∠ACB-∠B)
证明:(1)如图①所示,当高AE在三角形ABC内部时,
∵AE⊥BC于E,
∴∠B+∠BAE=90°(直角三角形两锐角互余)
∴∠BAE=90°-∠B
同理,∠CAE=90°-∠C
又∵AD平分∠BAC,∴∠BAD=∠CAD
∴∠BAE-∠CAE=2∠DAE=(90°-∠B)-(90°-∠C)=∠C-∠B.
∴∠DAE=$\frac{1}{2}$(∠ACB-∠B)
(2)如图②所示,当高AE在三角形外部时,还能得到∠DAE=$\frac{1}{2}(∠ACB-∠B)$吗?如果不能,请说明理由;如果能,请证明.
分析 由角平分线的定义可知∠2=$\frac{1}{2}$∠BAC,由直角三角形两锐角互余可知∠3=90°-∠ACE,由三角形的内角和定理可知∠BAC=180°-∠B-∠ACB,由三角形外角的性质得到∠ACE=∠B+∠BAC,最后根据∠DAE=∠2+∠3进行化简整理即可.
解答 解:∵AD是∠BAC的平分线,
∴∠2=$\frac{1}{2}$∠BAC.
∵AE为BC边上的高线,
∴∠3=90°-∠ACE.
∵∠BAC=180°-∠B-∠ACB,∠ACE=∠B+∠BAC,
∴∠DAE=$\frac{1}{2}$(180°-∠B-∠ACB)+90°-(∠B+∠BAC)
=$\frac{1}{2}$(180°-∠B-∠ACB)+90°-(∠B+180°-∠B-∠ACB)
=90°-$\frac{1}{2}∠B$-$\frac{1}{2}∠ACB$+90°-180°+∠ACB
=$\frac{1}{2}∠ACB-\frac{1}{2}∠B$.
=$\frac{1}{2}(∠ACB-∠B)$.
点评 本题主要考查的是角平分线的定义、三角形的内角和定理、三角形的外角的性质,利用三角形的内角和定理和外角的性质进行变形是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
4.某粮食加工厂从生产的粮食中抽出20袋检查质量,以每袋50千克为标准,将超过的千克数记为正数,不足的千克数记为负数,结果记录如下:
问:
(1)这20袋大米共超重或不足多少千克?
(2)这20袋大米的总质量为多少千克?平均每袋是多少千克?
| 与标准质量的偏差/千克 | -0.7 | -0.5 | -0.2 | 0 | +0.4 | +0.5 | +0.7 |
| 袋数 | 1 | 3 | 4 | 5 | 3 | 3 | 1 |
(1)这20袋大米共超重或不足多少千克?
(2)这20袋大米的总质量为多少千克?平均每袋是多少千克?
2.2015年2月1日,石家庄市区的最高气温是2℃,最低气温是-5℃,则该天的最高气温比最低气温高( )
| A. | -7℃ | B. | 7℃ | C. | -3℃ | D. | 3℃ |
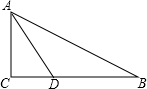 如图,在△ABC中,∠C=90°,∠B=30°,BC=6cm,AD是∠CAB的平分线,求DC的长.
如图,在△ABC中,∠C=90°,∠B=30°,BC=6cm,AD是∠CAB的平分线,求DC的长.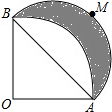 如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.
如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.