题目内容
16.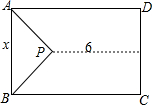 如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.
如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.
分析 过点P作PE⊥AB,垂足为E,由等腰直角三角形的性质可求得PE=$\frac{1}{2}x$,然后根据草地的面积=矩形的面积-△ABP的面积可求得函数关系式.
解答 解:过点P作PE⊥AB,垂足为E.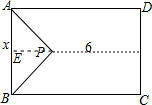
∵△ABP为等腰直角三角形,AP⊥BP,
∴PE=$\frac{1}{2}AB$=$\frac{1}{2}x$.
草地的面积=矩形的面积-△ABP的面积=x(6+$\frac{1}{2}$x)-$\frac{1}{2}x•\frac{1}{2}x$=$\frac{1}{4}{x}^{2}$+6x,
∴y与x的函数关系式为y=$\frac{1}{4}{x}^{2}+6x$.
点评 本题主要考查的是矩形的性质、等腰直角三角形,求函数的关系式,根据草地的面积=矩形的面积-△ABP的面积求解是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在某小区花园中有x棵月季花,茶花的数量比月季花的棵数的3倍多7棵,则茶花的棵树是( )
| A. | 3x-7 | B. | 3x+7 | C. | 7x-3 | D. | 7x+3 |
4.某粮食加工厂从生产的粮食中抽出20袋检查质量,以每袋50千克为标准,将超过的千克数记为正数,不足的千克数记为负数,结果记录如下:
问:
(1)这20袋大米共超重或不足多少千克?
(2)这20袋大米的总质量为多少千克?平均每袋是多少千克?
| 与标准质量的偏差/千克 | -0.7 | -0.5 | -0.2 | 0 | +0.4 | +0.5 | +0.7 |
| 袋数 | 1 | 3 | 4 | 5 | 3 | 3 | 1 |
(1)这20袋大米共超重或不足多少千克?
(2)这20袋大米的总质量为多少千克?平均每袋是多少千克?
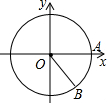 如图,以原点为圆心,2为半径的⊙O与正半轴交于点A,在⊙O上且在x轴的下方有一点B,∠AOB=45°,则点B的坐标为($\sqrt{2}$,$-\sqrt{2}$).
如图,以原点为圆心,2为半径的⊙O与正半轴交于点A,在⊙O上且在x轴的下方有一点B,∠AOB=45°,则点B的坐标为($\sqrt{2}$,$-\sqrt{2}$).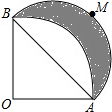 如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.
如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2. 如图,正方形纸片的边长为20cm,若将其相邻的两边长分别截去xcm和2xcm,求截取后所得的矩形面积y与x之间的函数关系式.
如图,正方形纸片的边长为20cm,若将其相邻的两边长分别截去xcm和2xcm,求截取后所得的矩形面积y与x之间的函数关系式.