题目内容
13.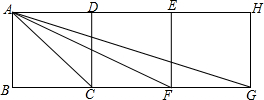 如图,四边形ABCD,CDEF,EFGH均是正方形,且B,C,F,G在一直线上,连接AC,AF,AG
如图,四边形ABCD,CDEF,EFGH均是正方形,且B,C,F,G在一直线上,连接AC,AF,AG(1)求证:△ACF∽△GCA;
(2)求∠AFB+∠AGB的度数.
分析 (1)由对应边成比例及其夹角相等可得三角形相似;
(2)由(1)可得∠AFB=∠CAF,进而可得其和的大小.
解答 解:(1)设正方形ABCD,DCFE,EFGH的边长为1,
∴CF=1,AC=$\sqrt{2}$,CG=2,
∵$\frac{AC}{CG}$=$\frac{\sqrt{2}}{2}$,$\frac{CF}{CA}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
又∵∠ACF=∠GCA,
∴△ACF∽△GCA;
(2)由(1)得:△ACF∽△GCA,
∴∠AFB=∠GAC,
∴∠AFB+∠AGB=∠GAC+∠AGB=∠ACB=45°.
点评 本题主要考查了正方形的性质及相似三角形的判定及性质问题,应熟练掌握.

练习册系列答案
相关题目
4.某粮食加工厂从生产的粮食中抽出20袋检查质量,以每袋50千克为标准,将超过的千克数记为正数,不足的千克数记为负数,结果记录如下:
问:
(1)这20袋大米共超重或不足多少千克?
(2)这20袋大米的总质量为多少千克?平均每袋是多少千克?
| 与标准质量的偏差/千克 | -0.7 | -0.5 | -0.2 | 0 | +0.4 | +0.5 | +0.7 |
| 袋数 | 1 | 3 | 4 | 5 | 3 | 3 | 1 |
(1)这20袋大米共超重或不足多少千克?
(2)这20袋大米的总质量为多少千克?平均每袋是多少千克?
2.2015年2月1日,石家庄市区的最高气温是2℃,最低气温是-5℃,则该天的最高气温比最低气温高( )
| A. | -7℃ | B. | 7℃ | C. | -3℃ | D. | 3℃ |
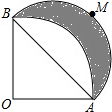 如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.
如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2. 如图,正方形纸片的边长为20cm,若将其相邻的两边长分别截去xcm和2xcm,求截取后所得的矩形面积y与x之间的函数关系式.
如图,正方形纸片的边长为20cm,若将其相邻的两边长分别截去xcm和2xcm,求截取后所得的矩形面积y与x之间的函数关系式.