题目内容
13．
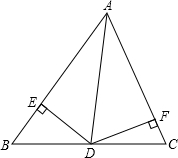如图，在△ABC中，AD为角平分线，DE⊥AB于E，DF⊥AC于F，AB=10cm，AC=8cm，△ABC的面积为45cm2，则DE的长为5cm．
分析 根据角平分线上的点到角的两边距离相等可得DE=DF，然后利用三角形的面积公式列方程求解即可．
解答 解：∵AD为角平分线，DE⊥AB于E，DF⊥AC于F，
∴DE=DF，
∵△ABC的面积为45cm2，
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=45，
∵AB=10cm，AC=8cm，
∴$\frac{1}{2}$×10×DE+$\frac{1}{2}$×8×DE=45，
解得DE=5cm．
故答案为：5．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，三角形的面积，熟记性质并利用三角形的面积列出方程是解题的关键．
练习册系列答案
相关题目
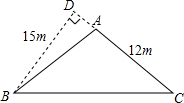如图所示，有一块三角形ABC空地，要在这块空地上种植草皮来美化环境，已知这种草皮每平方米售价300元，AC=12m，BD=15m．
如图是一个长与宽之比为2：1的长方形草坪，其对角线长为$\sqrt{125}$米，现欲改造成一个面积相等的正方形草坪，则改造后的正方形草坪的边长为5$\sqrt{2}$米．
a、b、c三个数在数轴上的对应位置如图所示，化简：|a|-|a+b|+|c-b|+|a+c|．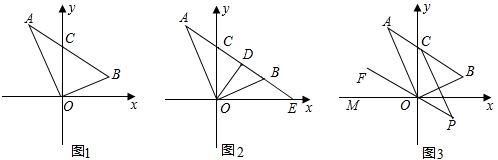
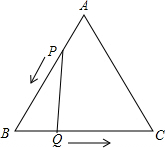如图所示，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（s），解答下列问题：