题目内容
12.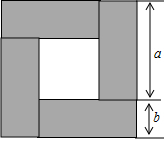 把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题:
把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题:(1)按要求用含、的两种方式表示空心部分的正方形的面积S(结果不要化简保留原式):
①用大正方形面积减去四块木板的面积表示:S=(a+b)2-4ab;
②直接用空心部分的正方形边长的平方表示:S=(a-b)2;
(2)由①、②可得等式(a+b)2-4ab=(a-b)2;
(3)试证明(2)中的等式成立.
分析 (1)①观察图形,可得图中大正方形的边长为a+b,每一块长方形木板的长为a,宽为b,根据正方形的面积=边长2,长方形的面积=长×宽即可求解;
②观察图形,可得图中空心部分的正方形边长为a-b,根据正方形的面积=边长2即可求解;
(2)根据空心部分的正方形的面积不变即可得到等式;
(3)利用完全平方公式证明即可.
解答 解:(1)①用大正方形面积减去四块木板的面积表示:S=(a+b)2-4ab.
故答案为(a+b)2-4ab;
②直接用空心部分的正方形边长的平方表示:S=(a-b)2.
故答案为(a-b)2;
(2)由①、②可得等式(a+b)2-4ab=(a-b)2.
故答案为(a+b)2-4ab=(a-b)2;
(3)∵左边=(a+b)2-4ab=a2+2ab+b2-4ab=a2-2ab+b2,
右边=(a-b)2=a2-2ab+b2,
∴左边=右边,
∴等式成立.
点评 此题考查完全平方公式的几何背景,利用面积、边的关系建立等量关系是解决问题的关键.

练习册系列答案
相关题目
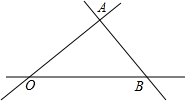 如图,三条公路OA,OB,AB两两相交于点O,点A和点B,现在建一个工厂P,使得工厂P到三条公路的距离相等
如图,三条公路OA,OB,AB两两相交于点O,点A和点B,现在建一个工厂P,使得工厂P到三条公路的距离相等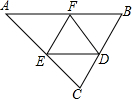 如图,在△ABC中,AB=6,AB边上的高为3,点F为AB上一点,点E为AC边上的一个动点,DE∥AB交BC于点D,若AB与DE之间的距离为x,则△DEF的面积y关于x的函数关系是3x-x2.
如图,在△ABC中,AB=6,AB边上的高为3,点F为AB上一点,点E为AC边上的一个动点,DE∥AB交BC于点D,若AB与DE之间的距离为x,则△DEF的面积y关于x的函数关系是3x-x2.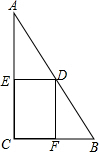 如图,在Rt△ABC中,已知∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F.得四边形DECF.设DE=x,DF=y
如图,在Rt△ABC中,已知∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F.得四边形DECF.设DE=x,DF=y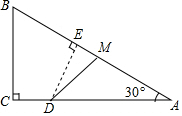 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y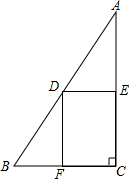 如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y. 如图所示,D是BC的中点,E是AC的中点,若S△ADE=1,则S△ABC=4.
如图所示,D是BC的中点,E是AC的中点,若S△ADE=1,则S△ABC=4.