题目内容
3.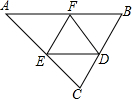 如图,在△ABC中,AB=6,AB边上的高为3,点F为AB上一点,点E为AC边上的一个动点,DE∥AB交BC于点D,若AB与DE之间的距离为x,则△DEF的面积y关于x的函数关系是3x-x2.
如图,在△ABC中,AB=6,AB边上的高为3,点F为AB上一点,点E为AC边上的一个动点,DE∥AB交BC于点D,若AB与DE之间的距离为x,则△DEF的面积y关于x的函数关系是3x-x2.
分析 根据相似三角形的对应边的比等于对应高的比等于相似比,用含x的代数式表示出ED,再用含x的代数式表示出S△DEF
解答  解:因为AB∥ED,
解:因为AB∥ED,
∴△CED∽△ABC
∴$\frac{DE}{AB}=\frac{3-x}{3}$
∴DE=2(3-x)
∴S△DEF=$\frac{1}{2}$DE×x
=$\frac{1}{2}$×2(3-x)×x
=3x-x2
故答案为:3x-x2
点评 本题考查了相似三角形的性质及二次函数的相关知识.解决本题的关键是利用相似三角的对应边的比等于对应高的比.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 已知平面直角坐标系中,点A(-3,3)、B(-2,-2).
已知平面直角坐标系中,点A(-3,3)、B(-2,-2).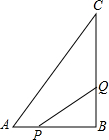 如图,△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A开始,沿AB边向点B以每秒1cm的速度移动;点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动.如果P,Q同时出发.
如图,△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A开始,沿AB边向点B以每秒1cm的速度移动;点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动.如果P,Q同时出发.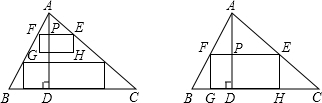 如图,△ABC中,BC=10cm,BC边上的高AD=8cm,E、F分别为AC、AB上的点,且EF∥BC,以EF为边向下作矩形EFGH,且满足EF=2FG,设EF的长为x(cm),矩形EFGH与△ABC重叠部分的面积为y(cm2).
如图,△ABC中,BC=10cm,BC边上的高AD=8cm,E、F分别为AC、AB上的点,且EF∥BC,以EF为边向下作矩形EFGH,且满足EF=2FG,设EF的长为x(cm),矩形EFGH与△ABC重叠部分的面积为y(cm2).
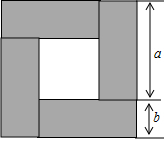 把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题:
把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题: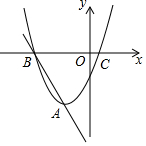 已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.
已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.