Question

5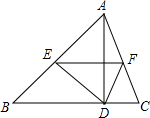．如图，在△ABC中，AD是高，将△ABC折叠，使点A和的D重合，折痕为EF，若AB=7cm，BC=6cm，AC=5cm，则△DEF的周长是9cm．

Answer 1

分析 根据折叠图形的对称性，易得△EDF≌△EAF，运用中位线定理可知△AEF的周长等于△ABC周长的一半，进而△DEF的周长可求解．

解答 解：∵△EDF是△EAF折叠以后形成的图形，
∴△EDF≌△EAF，
∴∠AEF=∠DEF，
∵AD是BC边上的高，
∴EF∥CB，
又∵∠AEF=∠B，
∴∠BDE=∠DEF，
∴∠B=∠BDE，
∴BE=DE，
同理，DF=CF，
∴EF为△ABC的中位线，
∴△DEF的周长为△EAF的周长，即AE+EF+AF=$\frac{1}{2}$（AB+BC+AC）=$\frac{1}{2}$（7+6+5）=9cm．
故答案为：9cm．

点评 本题考查了中位线定理，并涉及到图形的折叠，认识到图形折叠后所形成的图形△AEF与△DEF全等是解题的关键．